考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用f′(x0)=0是x0为函数f(x)极值点的必要而不充分条件,即可判断出.
B.利用特称命题的否定是全称命题即可得出;
C.利用三角形的内角和定理、正弦余弦函数的单调性、和差化积即可得出.
D.利用偶函数的定义即可判断出.
解答:
解:A.函数y=f(x)为R上的可导函数,则f′(x
0)=0是x
0为函数f(x)极值点的充要条件,错误.
导数为零的点不一定为极值点,例如函数f(x)=x
3,而f′(0)=0,但是此函数单调递增,无极值点;
B.命题“存在x∈R,x
2+x-1<0”的否定是“任意x∈R,x
2+x-1≥0”,因此B不正确;
C.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B”是真命题;其原因如下:∵0<B<A<A+B<π,∴
0<<,
0<<.
∴
cos>0,
sin>0.
∴sinA-sinB=
2cossin>0,即sinA>sinB.
D.“b=0”是“函数f(x)=ax
2+bx+c是偶函数”的充要条件,正确.
其原因如下:函数f(x)=ax
2+bx+c是偶函数?f(-x)=f(x)?2bx=0对于?x∈R都成立?b=0.
故选D
点评:本题综合考查了f′(x0)=0是x0为函数f(x)极值点的必要而不充分条件、特称命题的否定是全称命题、三角形的内角和定理、正弦余弦函数的单调性、和差化积、偶函数的定义等基础知识与基本技能方法,属于难题.



 名校课堂系列答案
名校课堂系列答案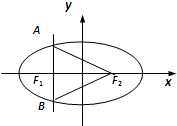 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆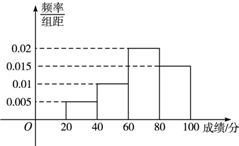 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( ) 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<