
分析 (1)代入计算,即可证明结论;
(2)由(1)可知,从第一项开始,每8项的和为0,即可求f(1)+f(2)+…+f(2020)的值.
解答 (1)证明:f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)+f(8)
=$sin\frac{π}{4}+sin\frac{2π}{4}+sin\frac{3π}{4}+sin\frac{4π}{4}+sin\frac{5π}{4}+sin\frac{6π}{4}+sin\frac{7π}{4}+sin\frac{8π}{4}$=$\frac{{\sqrt{2}}}{2}+1+\frac{{\sqrt{2}}}{2}+0+(-\frac{{\sqrt{2}}}{2})+(-1)+(-\frac{{\sqrt{2}}}{2})+0=0$,
f(9)+f(10)+…$+f(16)=sin\frac{9π}{4}+sin\frac{10π}{4}+sin\frac{10π}{4}+sin\frac{11π}{4}+$…$+sin\frac{15π}{4}+sin\frac{16π}{4}$=$sin\frac{π}{4}+sin\frac{2π}{4}+sin\frac{3π}{4}+$…$+sin\frac{7π}{4}+sin\frac{8π}{4}$=0
所以f(1)+f(2)+…+f(8)=f(9)+f(10)+…+f(16).
(2)解:由(1)可知,从第一项开始,每8项的和为0,
又∵2020=252×8+4
∴f(1)+f(2)+…+f(2020)=252×0+f(1)+f(2)+f(3)+f(4)=$\frac{{\sqrt{2}}}{2}+1+\frac{{\sqrt{2}}}{2}+0=1+\sqrt{2}$.
点评 本题考查函数的周期性及运用,考查三角函数的求值,考查运算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+lnn | B. | 2+(n-1)lnn | C. | lnn-2 | D. | 1+n+lnn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
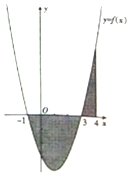
| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{9}{16}$ | B. | $-\frac{3}{4}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com