练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．某几何体的三视图如图所示，则其表面积为（　　）
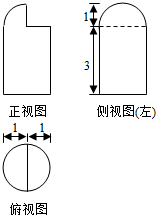
    A．$\frac{17π}{2}$B．9πC．$\frac{19π}{2}$D．10π

    分析 几何体为圆柱与$\frac{1}{4}$球的组合体．表面共有5部分组成．

    解答 解：由三视图可知几何体为圆柱与$\frac{1}{4}$球的组合体．
    圆柱的底面半径为1，高为3，球的半径为1．
    所以几何体的表面积为π×12+2π×1×3+$4π×{1}^{2}×\frac{1}{4}$+$\frac{1}{2}π×{1}^{2}$+$\frac{1}{2}π×{1}^{2}$=9π．
    故选B．

    点评 本题考查了圆柱与球的三视图，结构特征和面积计算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x，其中x∈（0，1），以A、B为焦点且过点D的双曲线的离心率为e1，以C、D为焦点且过点A的椭圆的离心率为e2，若对任意x∈（0，1），不等式t＜e1+e2恒成立，则t的最大值为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知焦点在x轴上的椭圆$\frac{x^2}{16}+\frac{y^2}{m}=1$的离心率为$\frac{1}{2}$，则m等于12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，离心率为e，过F2的直线与椭圆的交于A，B两点，若△F1AB是以A为顶点的等腰直角三角形，则e2=（　　）
    A．3-2$\sqrt{2}$B．5-3$\sqrt{2}$C．9-6$\sqrt{2}$D．6-4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，多面体SABCD中面ABCD为矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD，SD=$\sqrt{3}$AD．
    （I）求证：面SDB⊥面ABCD．
    （Ⅱ）求面SBD与面SAB所成的二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知$α∈（\frac{π}{2}，π）$，且sin（π+α）=-$\frac{3}{5}$，则tanα=（　　）
    A．$-\frac{3}{4}$B．$\frac{4}{3}$C．$\frac{3}{4}$D．$-\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．倾斜角为60°的直线l过抛物线y2=4x的焦点F，且与抛物线位于x轴上的部分相交于A，则△OFA的面积为（　　）
    A．$\frac{{\sqrt{3}}}{2}$B．$\frac{{2\sqrt{3}}}{3}$C．$\sqrt{3}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

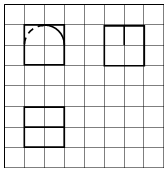    12．如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（　　）
    A．$6+\frac{π}{4}$B．$6+\frac{π}{2}$C．$6-\frac{π}{4}$D．$6-\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=l（a＞b＞0）的左、右焦点分别为F1、F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且2$\overrightarrow{{F_1}{F_2}}$+$\overrightarrow{{F_2}Q}$=0．
    （1）求椭圆C的离心率；
    （2）若过A、Q、F2三点的圆恰好与直线l：x-$\sqrt{3}$y-3=0相切，求椭圆C的方程；
    （3）在（2）的条件下，过右焦点F2作斜率为k的直线I与椭圆C交于M、N两点，在x轴上是否存在点P（m，0）使得以PM、PN为邻边的平行四边形是菱形，如果存在，求出m的取值范围；如果不存在，说明理由．

    查看答案和解析>>

    同步练习册答案