
分析 本题考查的知识点是必要条件、充分条件与充要条件的判断及不等式的性质,我们根据充要条件的定义对题目中的四个答案逐一进行分析即可得到答案.
解答 解:∵①中“a=b”⇒“ac=bc”为真命题,
但当c=0时,“ac=bc”⇒“a=b”为假命题,
故“a=b”是“ac=bc”的充分不必要条件,故①为假命题;
∵②中“a+5是无理数”⇒“a是无理数”为真命题,
“a是无理数”⇒“a+5是无理数”也为真命题,
故“a+5是无理数”是“a是无理数”的充要条件,故②为真命题;
∵③“(x-a)(x-b)=0”是“x=a”的必要条件,故③为假命题;
∵④中{a|a<5}?{a|a<3},故“a<5”是“a<3”的必要条件,故④为真命题.
故真命题的个数为2
故答案为:②④
点评 判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$∥($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {5} | C. | {3,4} | D. | {22,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,9] | B. | [5,+∞) | C. | $[\frac{{3\sqrt{2}}}{2},+∞)$ | D. | $[\frac{9}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0) | B. | -f′(x0) | C. | f(x0) | D. | -f(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
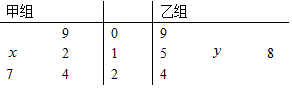 如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )
如图茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)已知甲组数据的中位数为5,乙组数据的平均数为6.8,则x,y的值分别为( )| A. | 2,5 | B. | 5,5 | C. | 5,8 | D. | 8,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com