Question

【题目】已知空间中三点A（－2,0,2），B（－1,1,2），C（－3,0,4），设a＝,b＝．

（1）求向量a与向量b的夹角的余弦值；

（2）若ka＋b与ka－2b互相垂直，求实数k的值

Answer 1

【答案】（1）;（2）或．

【解析】

试题分析：（1）第一步，求出两个向量的坐标，第二步，分别计算，和，最后代入公式；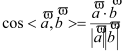

（2）方法一，先得到和的坐标，然后代入数量积的坐标表示，可得的值；

方法二，先计算（）（），然后代入两个向量的坐标表示，求的值．

试题解析：解 （1）∵a＝（1,1,0），b＝（－1,0,2）， ∴a·b＝（1,1,0）·（－1,0,2）＝－1，

又|a|＝＝， |b|＝＝，

∴cos〈a，b〉＝＝＝－， 即向量a与向量b的夹角的余弦值为－．

（2）方法一 ∵ka＋b＝（k－1，k,2）．ka－2b＝（k＋2，k，－4），且ka＋b与ka－2b互相垂直，

∴（k－1，k,2）·（k＋2，k，－4）＝（k－1）（k＋2）＋k2－8＝0， ∴k＝2或k＝－，

∴当ka＋b与ka－2b互相垂直时，实数k的值为2或－．、

方法二 由（1）知|a|＝，|b|＝，a·b＝－1，

∴（ka＋b）·（ka－2b）＝k2a2－ka·b－2b2＝2k2＋k－10＝0， 得k＝2或k＝－．