
分析 (1)△ABC是等腰三角形,建立平面直角坐标系,代入坐标计算各向量的坐标,模长,数量积,代入夹角公式计算夹角;
(2)由条件可知四边形ABCD是矩形,对角线为10,使用基本不等式即可求出面积的最大值.
解答 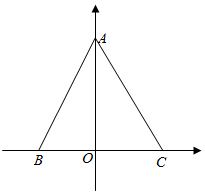 解:(1)∵|$\overrightarrow{AB}$|=$\sqrt{3}$|$\overrightarrow{BC}$|=|$\overrightarrow{AC}$|,∴△ABC是等腰三角形.
解:(1)∵|$\overrightarrow{AB}$|=$\sqrt{3}$|$\overrightarrow{BC}$|=|$\overrightarrow{AC}$|,∴△ABC是等腰三角形.
以BC所在直线为x轴,以BC边上的高所在直线为y轴家里平面直角坐标系
设B(-a,0),C(a,0),则A(0,$\sqrt{11}$a).
∴$\overrightarrow{CB}$=(-2a,0),$\overrightarrow{CA}$=(-a,$\sqrt{11}a$),$\overrightarrow{AC}=(a,-\sqrt{11}a)$,∴$\overrightarrow{CB}+\overrightarrow{CA}$=(-3a,$\sqrt{11}a$).
∴($\overrightarrow{CB}$+$\overrightarrow{CA}$)•$\overrightarrow{AC}$=-3a2-11a2=-14a2.
|$\overrightarrow{CB}+\overrightarrow{CA}$|=$\sqrt{9{a}^{2}+11{a}^{2}}$=2$\sqrt{5}$a,|$\overrightarrow{AC}$|=$\sqrt{{a}^{2}+11{a}^{2}}$=2$\sqrt{3}$a.
设$\overrightarrow{CB}$+$\overrightarrow{CA}$与$\overrightarrow{AC}$的夹角为θ,则cosθ=$\frac{-14{a}^{2}}{2\sqrt{5}a•2\sqrt{3}a}$=-$\frac{7\sqrt{15}}{30}$.
(2)∵$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$,且|$\overrightarrow{AB}$-$\overrightarrow{AD}$|=|$\overrightarrow{AC}$|=10,
∴四边形ABCD是对角线为10的矩形.
设AB=x,AD=y,则x2+y2=100≥2xy,∴xy≤50.当且仅当x=y=5$\sqrt{2}$时取等号.
∴四边形ABCD面积的最大值是50.
点评 本题考查了平面向量的数量积运算,向量线性运算的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
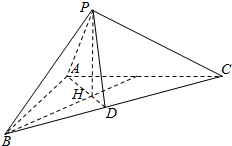 如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.
如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{2}$) | B. | (1,$\sqrt{2}$) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com