
分析 首先,$\frac{3sinα-cosα}{2sinα+3cosα}$的分子、分母同时除以cosα,并求得tanα=2.
(1)利用同角三角函数关系的关系来求tan($\frac{π}{2}$-α)的值;
(2)利用诱导公式,同角三角函数关系进行解答.
解答 解:∵$\frac{3sinα-cosα}{2sinα+3cosα}$=$\frac{5}{7}$,
∴$\frac{3sinα-cosα}{2sinα+3cosα}$=$\frac{3tanα-1}{2tanα+3}$=$\frac{5}{7}$.
解得,tanα=2.
(1)tan($\frac{π}{2}$-α)=cotα=$\frac{1}{tanα}$=$\frac{1}{2}$;
(2)原式=$\frac{3cosα•(-sinα)+2si{n}^{2}α}{si{n}^{2}α+co{s}^{2}α}$,
=$\frac{-3tanα+2ta{n}^{2}α}{1+ta{n}^{2}α}$,
=$\frac{-3×2+2×{2}^{2}}{1+{2}^{2}}$,
=$\frac{2}{5}$.
点评 本题主要考查三角函数的化简求值,三角函数中的恒等变换应用,利用三角函数公式将函数进行化简是解决本题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -2或6 | B. | 0或4 | C. | -1 或$\sqrt{3}$ | D. | -1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
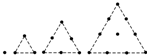 在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36,45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=$\frac{n(n+1)}{2}$.
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36,45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=$\frac{n(n+1)}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无极值点 | B. | 极大值点是$\frac{1}{e}$ | ||
| C. | 既有极大值点又有极小值点 | D. | 极小值点是$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 性别 专业 | 非统计专业 | 统计专业 |
| 男 | 15 | 10 |
| 女 | 5 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y′=3sin$\frac{1}{2}$x′ | B. | y′=$\frac{1}{3}$sin2x′ | C. | y′=$\frac{1}{2}$sin2x′ | D. | y′=3sin2x′ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com