
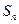 为数列
为数列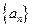 的前
的前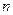 项和,对任意的
项和,对任意的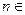 N
N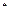 ,都有
,都有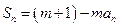
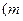 为常数,且
为常数,且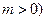 .
.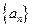 是等比数列;
是等比数列;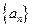 的公比
的公比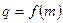 ,数列
,数列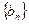 满足
满足
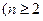 ,
,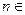 N
N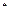
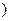 ,求数列
,求数列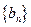 的通项公式;
的通项公式;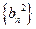 的前
的前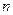 项和
项和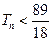 .
. 时,
时,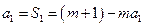 ,解得
,解得 .……………………………………1分
.……………………………………1分 时,
时, .……………………………………………2分
.……………………………………………2分 .
. 为常数,且
为常数,且 ,∴
,∴
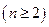 .………………………………………3分
.………………………………………3分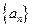 是首项为1,公比为
是首项为1,公比为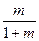 的等比数列.………………………………4分
的等比数列.………………………………4分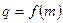
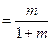 ,
, .……………………………5分
.……………………………5分 ,…………………………………………………………6分
,…………………………………………………………6分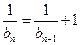 ,即
,即
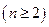 .………………………………………………7分
.………………………………………………7分 是首项为
是首项为 ,公差为1的等差数列.…………………………………………8分
,公差为1的等差数列.…………………………………………8分 ,即
,即 (
(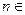 N
N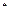 ).…………………………………………9分
).…………………………………………9分 ,则
,则 .……………………………10分
.……………………………10分
 ,……………………11分
,……………………11分 时,
时, ,………………………………………12分
,………………………………………12分

 .………………………………………………………14分
.………………………………………………………14分

科目:高中数学 来源:不详 题型:解答题
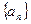 满足
满足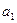 =-1,
=-1,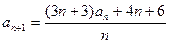 ,数列
,数列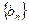 满足
满足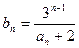
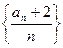 为等比数列,并求数列
为等比数列,并求数列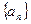 的通项公式.
的通项公式.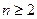 时,
时,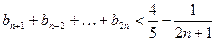
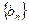 的前
的前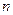 项和为
项和为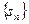 ,求证:当
,求证:当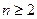 时,
时,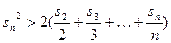 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.是原数列的第18项 | B.是原数列的第13项 |
| C.是原数列的第19项 | D.不是原数列中的项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com