
分析 ①当x≥-$\frac{a}{2}$时,方程可化为x2-4x-2a=0,从而可判断x2-4x-2a=0在[-$\frac{a}{2}$,+∞)上有两个不同的解,②当x<-$\frac{a}{2}$时,方程可化为x2+4x+2a=0,从而讨论确定方程在
(-∞,-$\frac{a}{2}$)上解的个数,从而确定实数a的取值范围.
解答 解:①当x≥-$\frac{a}{2}$时,
方程$\frac{1}{2}$x2=|2x+a|可化为x2-4x-2a=0,
当△=16+8a>0,即a>-2时,
x2-4x-2a=0在R上有两个不同的解,
又∵对称轴在区间(-$\frac{a}{2}$,+∞)上,
且$\frac{{a}^{2}}{4}$-2(2(-$\frac{a}{2}$)+a)=$\frac{{a}^{2}}{4}$≥0,
∴x2-4x-2a=0在[-$\frac{a}{2}$,+∞)上有两个不同的解,
②当x<-$\frac{a}{2}$时,
方程$\frac{1}{2}$x2=|2x+a|可化为x2+4x+2a=0,
当△=16-8a>0,即a<2时,
x2+4x+2a=0在R上有两个不同的解,
又∵对称轴在区间(-∞,-$\frac{a}{2}$)上,
且$\frac{{a}^{2}}{4}$-2(2(-$\frac{a}{2}$)+a)=$\frac{{a}^{2}}{4}$≥0,
当a≠0时,x2-4x-2a=0在(-∞,-$\frac{a}{2}$)上有两个不同的解,
当a=0时,x2-4x-2a=0在(-∞,-$\frac{a}{2}$)上只有一个解,
综上所述,方程$\frac{1}{2}$x2=|2x+a|有四个不同的解时,
-2<a<2且a≠0.
故答案为:-2<a<2且a≠0.
点评 本题考查了分类讨论的思想应用及绝对值方程的解法与应用.


科目:高中数学 来源: 题型:选择题
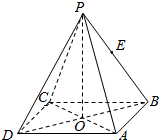 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 140 | B. | 280 | C. | 400 | D. | 420 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | -1或1 | D. | -1或$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 利润y | 5.8 | 6.6 | 7.1 | 7.4 | 8.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ+$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z | ||
| C. | [2kπ+$\frac{5π}{12}$,2kπ+$\frac{11π}{12}$],k∈Z | D. | [2kπ-$\frac{π}{12}$,2kπ+$\frac{5π}{12}$],k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com