
分析 (1)当a=1,b=3时,f(x)=x2+4x+2,由x2+4x+2=x,解得答案;
(2)令ax2+(b+1)x+b-1=x,则ax2+bx+b-1=0 ①,则方程①恒有两个不等实根,即b2-4ab+4a>0恒成立,则△′=16a2-16<0,解得a的取值范围;
(3)在(2)的条件下,x1+x2=-$\frac{b}{a}$=$\frac{2a}{5{a}^{2}-4a+1}$,即b=$\frac{-2{a}^{2}}{5{a}^{2}-4a+1}$=$\frac{-2}{(\frac{1}{a}-2)^{2}+1}$,进而得到b的最小值.
解答 解:(1)当a=1,b=3时,f(x)=x2+4x+2,
由x2+4x+2=x,
解得x=-2或x=-1,
所以所求的不动点为-1或-2.
(2)令ax2+(b+1)x+b-1=x,则ax2+bx+b-1=0 ①
由题意,方程①恒有两个不等实根,所以△=b2-4a(b-1)>0,
即b2-4ab+4a>0恒成立,
则△′=16a2-16<0,
故0<a<1
(3)设A(x1,x1),B(x2,x2)(x1≠x2),g(x)=-x+$\frac{2a}{5{a}^{2}-4a+1}$,
又AB的中点在该直线上,所以$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{{x}_{1}+{x}_{2}}{2}$+$\frac{2a}{5{a}^{2}-4a+1}$,
∴x1+x2=-$\frac{b}{a}$=$\frac{2a}{5{a}^{2}-4a+1}$,
∴b=$\frac{-2{a}^{2}}{5{a}^{2}-4a+1}$=$\frac{-2}{(\frac{1}{a}-2)^{2}+1}$
∴当 a=$\frac{1}{2}$∈(0,1)时,bmin=-2.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
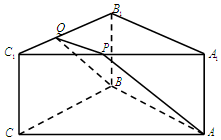 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com