
(本小题满分13分)如图所示的“8”字形曲线是由两个关于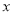 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是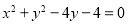 ,双曲线的左、右顶点
,双曲线的左、右顶点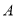 、
、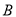 是该圆与
是该圆与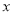 轴的交点,双曲线与半圆相交于与
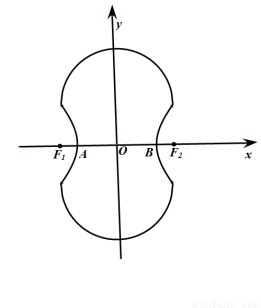
轴的交点,双曲线与半圆相交于与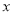 轴平行的直径的两端点.
轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为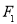 、
、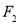 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点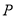 ,使得
,使得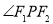 是直角.
是直角.
(1)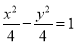 ;(2)
;(2)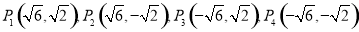
都可使得 是直角.
是直角.
【解析】
试题分析:(1)双曲线的左、右顶点 、
、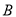 是该圆与
是该圆与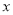 轴的交点,可令
轴的交点,可令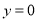 ,得到双曲线左、右顶点为
,得到双曲线左、右顶点为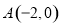 、
、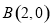 ,即
,即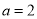 ,令
,令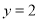 ,得到双曲线过点
,得到双曲线过点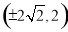 ,
,
即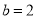 .
.
进而求得双曲线方程为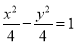 ;
;
(2)要使 是直角,则应使
是直角,则应使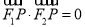 ,为此可设点
,为此可设点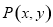 ,由(1)得双曲线的两个焦点
,由(1)得双曲线的两个焦点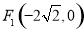 ,
,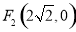 ,由向量数量积的坐标表示,得
,由向量数量积的坐标表示,得
,此时应分两种情况考虑点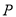 的位置:点
的位置:点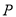 在双曲线上,联立
在双曲线上,联立 ,点
,点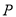 在上半圆上,联立
在上半圆上,联立 解出方程组的解即为点
解出方程组的解即为点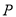 的坐标.试题解析:(1)设双曲线的方程为
的坐标.试题解析:(1)设双曲线的方程为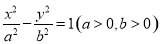 ,在已知圆的方程中,令
,在已知圆的方程中,令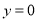 ,
,
得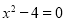 ,即
,即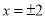 ,则双曲线左、右顶点为
,则双曲线左、右顶点为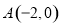 、
、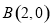 ,于是
,于是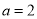 2分
2分
令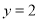 ,可得
,可得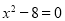 ,解得
,解得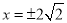 ,
,
即双曲线过点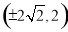 ,则
,则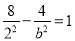 ∴
∴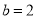 . 4分
. 4分
所以所求双曲线方程为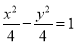 6分
6分
(2)由(1)得双曲线的两个焦点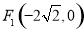 ,
,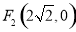 7分
7分
当 时,设点
时,设点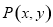 ,
,
①点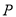 在双曲线上,得
在双曲线上,得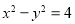 ,
,
由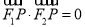 ,得
,得 由
由 ,解得
,解得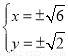 所以
所以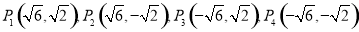 10分
10分
②若点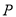 在上半圆上,则
在上半圆上,则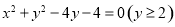 ,由
,由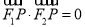 ,
,
得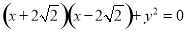 ,由
,由 无解 12分
无解 12分
综上,满足条件的点有4个,分别为
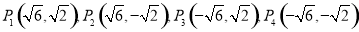 13分
13分
考点:1、双曲线的标准方程;2、向量数量积的坐标表示.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)设函数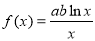 ,
,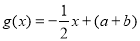 (其中
(其中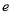 为自然对数的底数,
为自然对数的底数,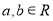 且
且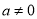 ),曲线
),曲线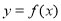 在点
在点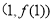 处的切线方程为
处的切线方程为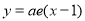 .
.
(1)求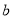 的值;
的值;
(2)若对任意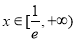 ,
,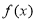 与
与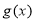 有且只有两个交点,求
有且只有两个交点,求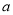 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检文科数学试卷(解析版) 题型:选择题
设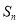 为公差不为零的等差数列
为公差不为零的等差数列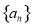 的前
的前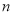 项和,若
项和,若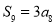 ,则
,则 ( )
( )
A. 15 B. 17 C. 19 D. 21
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检理科数学试卷(解析版) 题型:选择题
已知双曲线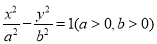 两个焦点为分别为
两个焦点为分别为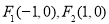 ,过点
,过点 的直线
的直线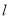 与该双曲线的右支交于
与该双曲线的右支交于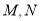 两点,且
两点,且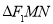 是以
是以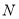 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则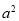 为( )
为( )
A.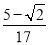 B.
B.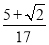 C.
C.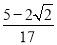 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省景德镇高三第二质检理科数学试卷(解析版) 题型:选择题
设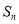 为公差不为零的等差数列
为公差不为零的等差数列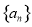 的前
的前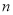 项和,若
项和,若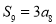 ,则
,则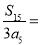 ( )
( )
A.15 B.17 C.19 D.21
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试文科数学试卷(解析版) 题型:选择题
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的外接球的半径是( ).

A. B.
B. C.2 D.
C.2 D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试理科数学试卷(解析版) 题型:选择题
把函数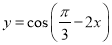 的图象向右平移
的图象向右平移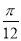 ,得到函数
,得到函数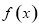 的图象,则函数
的图象,则函数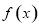 为( )
为( )
A.周期为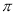 的奇函数 B.周期为
的奇函数 B.周期为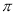 的偶函数
的偶函数
C.周期为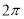 的奇函数 D.周期为
的奇函数 D.周期为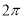 的偶函数
的偶函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com