
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | 16 | 16 | 14 | 14 | 4 |
分析 (Ⅰ)由20人中答对第5题的人数为4人,求出第5题的实测难度为0.2,由此能估计240人中实测答对人数.
(Ⅱ)X的可能取值是0,1,2.分别求出相应概率,由此能求出X的分布列和数学期望.
(Ⅲ)将抽样的20名学生中第i题的实测难度,作为240名学生第i题的实测难度.由题设条件推导出该次测试的难度预估是合理的.
解答 (本小题满分13分)
解:(Ⅰ)因为20人中答对第5题的人数为4人,因此第5题的实测难度为$\frac{4}{20}=0.2$.[(2分)]
所以,估计240人中有240×0.2=48人实测答对第5题.[(3分)]
(Ⅱ)X的可能取值是0,1,2.[(4分)]$P(X=0)=\frac{{C_{16}^2}}{{C_{20}^2}}=\frac{12}{19}$; $P(X=1)=\frac{{C_{16}^1C_4^1}}{{C_{20}^2}}=\frac{32}{95}$; $P(X=2)=\frac{C_4^2}{{C_{20}^2}}=\frac{3}{95}$.[(7分)]X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{12}{19}$ | $\frac{32}{95}$ | $\frac{3}{95}$ |
点评 本题考查概率的求法及应用,考查离散型随机变量的分布列和数学期望的求法,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题

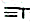 ”表示36,“
”表示36,“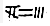 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )| A. |  | B. | 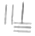 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x与y正相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y负相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.
如图,约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$,若在可行域△ABC上有无穷多个点(x,y),使得目标函数z=x+my取得最小值,求m的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
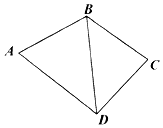 四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.
四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com