
 ��֪��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$����Բ���Ҷ���ֱ�ΪA��B����A����Բ������ľ���֮��Ϊ4����PΪ��Բ�ϲ�ͬ��A��B����һ�㣬��PQ��x�ᣬQΪ���㣮MΪ�߶�PQ�е㣬ֱ��AM��ֱ��l��x=b�ڵ�C��DΪ�߶�BC�е㣨��ͼ����
��֪��Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1��a��b��0����������e=$\frac{{\sqrt{3}}}{2}$����Բ���Ҷ���ֱ�ΪA��B����A����Բ������ľ���֮��Ϊ4����PΪ��Բ�ϲ�ͬ��A��B����һ�㣬��PQ��x�ᣬQΪ���㣮MΪ�߶�PQ�е㣬ֱ��AM��ֱ��l��x=b�ڵ�C��DΪ�߶�BC�е㣨��ͼ�������� ��1��������ɵã�$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2a=4}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$��������ɵó���
��2��A��-1��0����B��1��0����ֱ��l��x=1�����P��x0��y0�����ɵõ�M����P������Բ���̿ɵ�$4x_0^2+y_0^2=4$���ó�ֱ��AM�ķ��̣���x=1����C��1��$\frac{y_0}{{{x_0}+1}}$�����ɵ�D��1��$\frac{y_0}{{2��{x_0}+1��}}$����������������ֱ���������Ĺ�ϵ����֤����
��� �⣺��1��������ɵã�$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2a=4}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$��
����Բ�ķ���Ϊ$\frac{y^2}{4}+{x^2}=1$��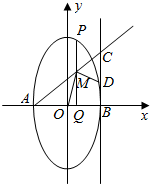
��2��֤����A��-1��0����B��1��0����ֱ��l��x=1��
���P��x0��y0�����ɵõ�$M��{x_0}��\frac{y_0}{2}��$����$4x_0^2+y_0^2=4$��
ֱ��AM��$y=\frac{y_0}{{2��{x_0}+1��}}��x+1��$����x=1����C��1��$\frac{y_0}{{{x_0}+1}}$������D��1��$\frac{y_0}{{2��{x_0}+1��}}$����
��$\overrightarrow{OM}=��{x_0}��\frac{y_0}{2}��$��$\overrightarrow{DM}=��{x_0}-1��\frac{y_0}{2}-\frac{y_0}{{2��{x_0}+1��}}��=��{x_0}-1��\frac{{{x_0}{y_0}}}{{2��{x_0}+1��}}��$��
��$\overrightarrow{OM}•\overrightarrow{DM}=��{x_0}��\frac{y_0}{2}��•��{x_0}-1��\frac{{{x_0}{y_0}}}{{2��{x_0}+1��}}��={x_0}��{x_0}-1��+\frac{{{x_0}y_0^2}}{{4��{x_0}+1��}}=\frac{{{x_0}��4x_0^2-4+y_0^2��}}{{4��{x_0}+1��}}$��
��$4{x}_{0}^{2}+{y}_{0}^{2}$=4����$\overrightarrow{OM}•\overrightarrow{DM}$=0��
���OMD=90�㣮
�ʡ�OMD��ֱ�������Σ�
���� ���⿼����Բ���ߵı����̼������ʡ�ֱ������Բ�ཻ���⡢������ֱ��������ֱ֮��Ĺ�ϵ���е����깫ʽ�Ȼ���֪ʶ��������ܣ���������������������������������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{4}$ | B�� | $\frac{127}{64}$ | C�� | $\frac{9}{4}$ | D�� | $\frac{129}{64}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
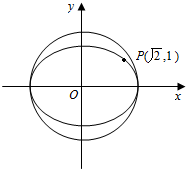 ��ͼ����Բ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������������˫����x2-y2=4�������ʻ�Ϊ��������������Բx2+y2=4��
��ͼ����Բ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������������˫����x2-y2=4�������ʻ�Ϊ��������������Բx2+y2=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com