
���� ��1���������֪�������־ͽ����Ҽ�ʤ�����һ���ڶ��ֱ������Ǽ�ʤ���ɴ�������������־ͽ����Ҽ�ʤ�ĸ��ʣ�
��2��������֪ǰ���ֱ���Ϊƽ�֣����������ľֱ���Ϊͬһ����ʤ���ɴ������ǡ�ñ����ľֽ����ĸ��ʣ�
��3��������֪���������������е�һ���ڶ��ֱ�������Ϊƽ�֣����������ı�������ҲΪƽ�֣����塢�����ֶ�Ϊ��ʤ�������ڵ�һ���ڶ��ֱ�������Ϊƽ�֣����������ľֱ�������ҲΪƽ�֣����塢�����ֱ���Ϊƽ�ֵ���һ���Ǽ�ʤ���ɴ��������ʤ�ĸ��ʣ�
��� �⣺��1���������֪�������־ͽ����Ҽ�ʤ�����һ���ڶ��ֱ������Ǽ�ʤ��
��������־ͽ����Ҽ�ʤ�ĸ���Ϊ$P=\frac{2}{3}��\frac{2}{3}=\frac{4}{9}$������3�֣�
��2��������֪ǰ���ֱ���Ϊƽ�֣����������ľֱ���Ϊͬһ����ʤ��
��ǡ�ñ����ľֽ����ĸ���Ϊ$P=C_2^1��{\frac{2}{3}}����{\frac{1}{3}}����{{{��{\frac{2}{3}}��}^2}+{{��{\frac{1}{3}}��}^2}}��$=$\frac{20}{81}$������7�֣�
��3��������֪���������������е�һ���ڶ��ֱ�������Ϊƽ�֣�
���������ı�������ҲΪƽ�֣����塢�����ֶ�Ϊ��ʤ��
�����ڵ�һ���ڶ��ֱ�������Ϊƽ�֣����������ľֱ�������ҲΪƽ�֣�
���塢�����ֱ���Ϊƽ�ֵ���һ���Ǽ�ʤ��
�����������������У���ʤ�ĸ���Ϊ$P={[{C_2^1��{\frac{2}{3}}����{\frac{1}{3}}��}]^2}{��{\frac{2}{3}}��^2}+��{\frac{2}{3}}����{\frac{1}{3}}��{[{C_2^1��{\frac{2}{3}}����{\frac{1}{3}}��}]^2}=\frac{32}{243}$������12�֣�
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע��������¼����ʳ˷���ʽ�������¼����ʼӷ���ʽ�ĺ������ã�


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | n | 4 | 4.5 |
| A�� | 3 | B�� | 3.15 | C�� | 3.5 | D�� | 4.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
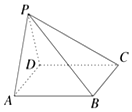 ��ͼ��������P-ABCD�У�����PAD�DZ߳�Ϊ4���������Σ�����ABCDΪ�����Σ�����PAD�͵���ABCD��MΪ����ABCD�ڵ�һ�����㣬������$\overrightarrow{MP}•\overrightarrow{MC}=0$�����M��ֱ��AB����̾���Ϊ��������
��ͼ��������P-ABCD�У�����PAD�DZ߳�Ϊ4���������Σ�����ABCDΪ�����Σ�����PAD�͵���ABCD��MΪ����ABCD�ڵ�һ�����㣬������$\overrightarrow{MP}•\overrightarrow{MC}=0$�����M��ֱ��AB����̾���Ϊ��������| A�� | $\sqrt{5}$ | B�� | $4-\sqrt{5}$ | C�� | $3-\sqrt{5}$ | D�� | $4-2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [k��-$\frac{��}{3}$��k��+$\frac{��}{6}$]��k��Z�� | B�� | $[{k��k��+\frac{��}{2}}]��{k��Z}��$ | C�� | $[{k��+\frac{��}{6}��k��+\frac{2��}{3}}]��{k��Z}��$ | D�� | $[{k��-\frac{��}{2}��k��}]��{k��Z}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}}{3}$ | B�� | $\frac{\sqrt{6}}{3}$ | C�� | $\frac{\sqrt{3}}{4}$ | D�� | $\frac{\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com