
分析 求得f(x)的导数,设(x1,y1)为f(x)上的任一点,可得切线的斜率k1,求得g(x)的导数,设g(x)图象上一点(x2,y2)可得切线l2的斜率为k2,运用两直线垂直的条件:斜率之积为-1,分别求y1=2a+cosx2的值域A,y2═$\frac{1}{{e}^{{x}_{1}}+1}$值域B,由题意可得B⊆A,可得a的不等式,可得a的范围.
解答 解:f(x)=-ex-x的导数为f′(x)=-ex-1,
设(x1,y1)为f(x)上的任一点,
则过(x1,y1)处的切线l1的斜率为k1=-ex1-1,
g(x)=2ax+sinx的导数为g′(x)=2a+cosx,
过g(x)图象上一点(x2,y2)处的切线l2的斜率为k2=2a+cosx2.
由l1⊥l2,可得(-ex1-1)•(2a+cosx2)=-1,
即2a+cosx2=$\frac{1}{{e}^{{x}_{1}}+1}$,
任意的x1∈R,总存在x2∈R使等式成立.
则有y1=2a+cosx2的值域为A=[2a-1,2a+1].
y2=$\frac{1}{{e}^{{x}_{1}}+1}$的值域为B=(0,1),
有B⊆A,即(0,1)⊆[2a-1,2a+1].
即$\left\{\begin{array}{l}{2a-1≤0}\\{2a+1≥1}\end{array}\right.$,
解得0≤a≤$\frac{1}{2}$.
故答案为:[0,$\frac{1}{2}$].
点评 本题考查导数的运用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,考查任意存在性问题的解法,注意运用转化思想和值域的包含关系,考查运算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥β,那么平面α 中一定存在直线平行于平面β | |
| C. | 如果平面 α不垂直于平面β,那么平面α 内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥β,那么平面 α内所有直线都垂直于平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
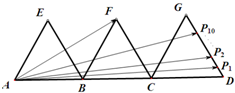 如图,三个边长为2的等边三角形有一条边在同一条直线上,边GD上有10个不同的点P1,P2,P3…P10,则$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180.
如图,三个边长为2的等边三角形有一条边在同一条直线上,边GD上有10个不同的点P1,P2,P3…P10,则$\overrightarrow{AF}$•($\overrightarrow{A{P_1}$+$\overrightarrow{A{P_2}}$+$\overrightarrow{A{P_3}}$+…+$\overrightarrow{A{P_{10}}}$)=180.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9π | B. | $\frac{49}{4}π$ | C. | 16π | D. | $\frac{81}{4}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com