
分析 (1)设∠ADE=θ,根据平面向量的数量积公式得到所求;
(2)设∠EDC=α,由数量积公式分析$\overrightarrow{DE}•\overrightarrow{DC}$的最大值的意义.
解答 解:(1)设∠ADE=θ,根据平面向量的数量积公式$\overrightarrow{DE}•\overrightarrow{CB}=\overrightarrow{DE}•\overrightarrow{DA}$=$|\overrightarrow{DE}|•|\overrightarrow{DA}|cosθ$,
由正方形ABCD的边长为2,点E是AB边上的动点可知,$|\overrightarrow{DE}|•cosθ=|\overrightarrow{DA}|$,
因此$\overrightarrow{DE}•\overrightarrow{CB}=|\overrightarrow{DA}{|^2}=4$;
(2)设∠EDC=α,$\overrightarrow{DE}•\overrightarrow{DC}=|\overrightarrow{DE}|•|\overrightarrow{DC}|cosα$=2$|\overrightarrow{DE}|•cosα$,而$|\overrightarrow{DE}|•cosα$就是向量$\overrightarrow{DE}$在$\overrightarrow{DC}$边上的射影,
要想让$\overrightarrow{DE}•\overrightarrow{DC}$最大,即让射影最大,此时E点与B点重合,射影为$\overrightarrow{DC}$,所以$\overrightarrow{DE}•\overrightarrow{DC}$的最大值为2.
点评 本题考查了向量的数量积公式的运用;熟练掌握公式是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
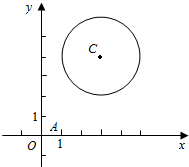 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\frac{1}{2}$ | B. | m≥2 | C. | 0<m<2 | D. | 0<m<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com