
分析 求出焦点坐标和准线方程,把|PA|+|PF|转化为PA|+|PM|,利用 当P、A、M三点共线时,|PA|+|PF|取得最小值,
把y=2代入抛物线y2=2x,解得x值,即得P的坐标.
解答 解:由题意得 F($\frac{1}{2}$,0),准线方程为 x=-$\frac{1}{2}$,设点P到准线的距离为d=|PM|,
则由抛物线的定义得|PA|+|PF|=|PA|+|PM|,
故当P、A、M三点共线时,|PA|+|PF|取得最小值为|AM|=3-(-$\frac{1}{2}$)=$\frac{7}{2}$.
把 y=2代入抛物线y2=2x 得 x=2,故点P的坐标是(2,2),
故答案为:(2,2).
点评 本题考查抛物线的定义和性质得应用,体现了转化的数学思想.


科目:高中数学 来源: 题型:选择题
| A. | a<b | B. | a=b | ||
| C. | a>b | D. | a,b的大小与n的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
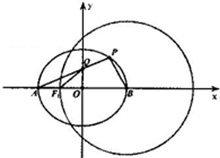 如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.
如图,点A,B分别是椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,圆B:(x-2)2+y2=9,经过椭圆E的左焦点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin x | B. | -cos x | C. | sin x | D. | cos x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
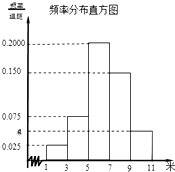 为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com