
分析 先求出A,B的坐标,可得AB中点坐标,利用点P(-m,0)满足|PA|=|PB|,可得$\frac{\frac{3m{b}^{2}}{9{b}^{2}-{a}^{2}}-0}{\frac{m{a}^{2}}{9{b}^{2}-{a}^{2}}+m}$=-3,从而可求双曲线的渐近线方程.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线方程为y=±$\frac{b}{a}$x,则
与直线x-3y+m=0联立,可得A($\frac{ma}{3b-a}$,$\frac{mb}{3b-a}$),B(-$\frac{ma}{3b+a}$,$\frac{mb}{3b+a}$),
∴AB中点坐标为($\frac{m{a}^{2}}{9{b}^{2}-{a}^{2}}$,$\frac{3m{b}^{2}}{9{b}^{2}-{a}^{2}}$),
∵点P(-m,0)满足|PA|=|PB|,
∴$\frac{\frac{3m{b}^{2}}{9{b}^{2}-{a}^{2}}-0}{\frac{m{a}^{2}}{9{b}^{2}-{a}^{2}}+m}$=-3,
∴a=b,
∴双曲线的渐近线方程为y=±x.
故答案为:y=±x.
点评 本题考查双曲线的渐近线方程,考查直线与双曲线的位置关系,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 540 | B. | 720 | C. | 3240 | D. | 4320 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$=M | B. | $\sqrt{ab}$=M | C. | a+b=M | D. | ab=M |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-1,1] | C. | [0,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
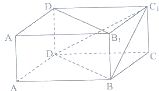
| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com