
分析 要使得f(x)有意义,则有$\left\{\begin{array}{l}{2x-1≥0}\\{x≠0}\end{array}\right.$,这样即可得出f(x)的定义域;可令$\sqrt{2x-1}=t$,从而得到$x=\frac{{t}^{2}+1}{2}$,t≥0,从而有$y=\frac{2t}{{t}^{2}+1}$,可讨论t:t=0时,y=0,而t>0时,有$y=\frac{2}{t+\frac{1}{t}}$,这样根据基本不等式便可求出y的范围,从而得出函数f(x)的值域.
解答 解:解$\left\{\begin{array}{l}{2x-1≥0}\\{x≠0}\end{array}\right.$得,$x≥\frac{1}{2}$;
∴f(x)的定义域为$[\frac{1}{2},+∞)$;
令$\sqrt{2x-1}=t$,t≥0,∴$x=\frac{{t}^{2}+1}{2}$,设y=f(x),则:
$y=\frac{2t}{{t}^{2}+1}$;
①若t=0,y=0;
②若t>0,则$y=\frac{2}{t+\frac{1}{t}}$;
$t+\frac{1}{t}≥2$,t=1时取“=”;
∴0<y≤1;
∴0≤y≤1;
∴f(x)的值域为[0,1].
故答案为:$[\frac{1}{2},+∞),[0,1]$.
点评 考查函数定义域、值域的概念及求法,换元法求函数的值域,以及基本不等式的运用.


科目:高中数学 来源: 题型:选择题
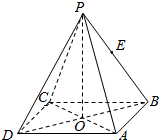 如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$,若E是PB的中点,则异面直线PD与AE所成角的正切值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方体、球、侧棱两两垂直且相等的正三棱锥 | |
| B. | 正方体、球、各棱长都相等的正三棱柱 | |
| C. | 球、高和底面半径相等的圆柱、高和底面半径相等的圆锥 | |
| D. | 正方体、正四棱台、棱长相等的平行六面体 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 利润y | 5.8 | 6.6 | 7.1 | 7.4 | 8.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com