

分析 先根据算法语句确定该算法程序的功能是计算分段函数的函数值,再根据题意求出分段函数的解析式.
解答 解:输入x由算法程序可知,
当x≤3时,y=2x,
当x>3时,y=x2-1,
综上所述,y=$\left\{\begin{array}{l}{2x,x≤3}\\{{x}^{2}-1,x>3}\end{array}\right.$,
故答案为y=$\left\{\begin{array}{l}{2x,x≤3}\\{{x}^{2}-1,x>3}\end{array}\right.$.
点评 本题考查了算法的程序语句问题,语句的识别问题是一个逆向性思维,如果将程序摆在我们的面前时,要从识别逐个语句,整体把握,概括程序的功能.属于基础题.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
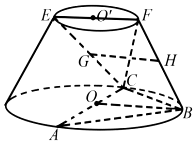 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=P | B. | M?P | ||
| C. | P?M | D. | M与P没有公共元素 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com