
(1)设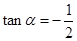 ,求
,求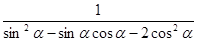 的值;
的值;
(2)已知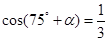 ,且
,且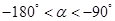 ,求
,求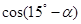 的值.
的值.
(1)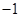 ;(2)
;(2)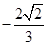 .
.
解析试题分析:(1)将所求式分子1换成 ,然后分子分母同除以
,然后分子分母同除以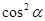 ,将其转化为关于
,将其转化为关于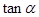 的式子再进行计算即可,本题若由
的式子再进行计算即可,本题若由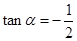 ,去求出
,去求出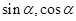 ,则需要讨论,若想不到用
,则需要讨论,若想不到用 代替1,则可原式分子分母同除以
代替1,则可原式分子分母同除以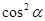 ,然后再考虑求出
,然后再考虑求出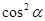 ,显然这两种方法较为麻烦;(2)此类给三角函数值求三角函数值的问题一般是通过考察条件中的角和问题中的角的关系,然后通过诱导公式、同角三角函数关系式、和差角公式进行计算.注意到
,显然这两种方法较为麻烦;(2)此类给三角函数值求三角函数值的问题一般是通过考察条件中的角和问题中的角的关系,然后通过诱导公式、同角三角函数关系式、和差角公式进行计算.注意到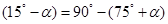 ,由诱导公式知
,由诱导公式知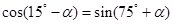 ,结合条件由同角三角函数关系式可求出
,结合条件由同角三角函数关系式可求出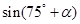 ,注意公式使用时要考察角的范围从而确定三角函数值的符号.
,注意公式使用时要考察角的范围从而确定三角函数值的符号.
试题解析:(1)原式=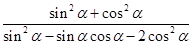 3分
3分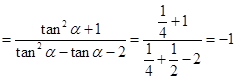 7分
7分
(2)由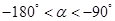 ,得
,得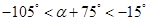 ,
,
故 10分
10分
而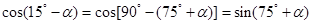
所以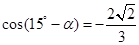 14分
14分
考点:同角三角函数的关系、三角函数的诱导公式.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
如图所示,一个半圆和长方形组成的铁皮,长方形的边 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边 .
.
(1)设 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
①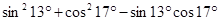 ;
;
②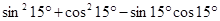 ;
;
③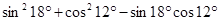 ;
;
④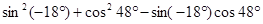 ;
;
⑤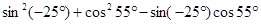 .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com