
分析 (1)(2)分别由根式内部的代数式大于等于0,分式的分母不为0求解不等式组可得答案;
(3)由函数y=f(x2-1)定义域求得f(x)的定义域,再由2x+1在f(x)的定义域内求得x的范围得答案.
解答 解:(1)由$\left\{\begin{array}{l}{{x}^{2}+x-1≥0}\\{{x}^{2}-2x+1≠0}\end{array}\right.$,解得$x≤\frac{-1-\sqrt{5}}{2}$,或$x≥\frac{-1+\sqrt{5}}{2}$且x≠1.
∴函数f(x)=$\sqrt{{x^2}+x-1}$+$\frac{1}{{{x^2}-2x+1}}$的定义域为(-∞,$\frac{-1-\sqrt{5}}{2}$]∪[$\frac{-1+\sqrt{5}}{2}$,1)∪(1,+∞);
(2)由$\left\{\begin{array}{l}{|x-2|-1≥0}\\{(x-3)(x-1)≠0}\end{array}\right.$,解得x<1或x>3.
∴函数f(x)=$\frac{{\sqrt{|{x-2}|-1}}}{(x-3)(x-1)}$的定义域为(-∞,1)∪(3,+∞);
(3)由题意,-1≤x≤3,∴,2≤x-1≤2,故f(x)的定义域为[-2,2],
∴令-2≤2x+1≤2,解得$-\frac{3}{2}≤x≤\frac{1}{2}$,
故y=f(2x+1)的定义域是[-$\frac{3}{2},\frac{1}{2}$].
点评 本题考查函数的定义域及其求法,考查不等式组的解法,是基础的计算题.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\frac{{\sqrt{3}}}{3}]∪$(1,+∞) | C. | $[\frac{{\sqrt{3}}}{3},1)$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
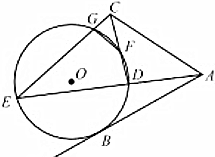 如图,AB是圆O的一条切线,切点为B,直线ABD,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,直线ABD,CFD,CGE都是圆O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
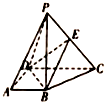 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,CD=2AB=2AD=2,PB⊥底面ABCD,E是PC上的点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,CD=2AB=2AD=2,PB⊥底面ABCD,E是PC上的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com