
如图所示,在圆锥PO中, PO= ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.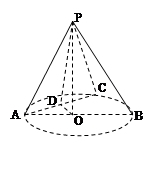
(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
(1)见解析;(2)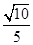
解析试题分析:(1)通过证平面PAC内直线AC^平面POD,由平面与平面垂直的判定定理得平面PAC^平面POD;(2)用垂面法作出二面角的平面角,然后在直角三角形中利用边长求平面角的余弦值.
试题解析:证明:(1)如图所示,连接OC.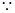 OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,
OA=OC,D是AC的中点,\AC^OD,在圆锥PO中,PA=PC,
则AC^PD,又PDÇOD=D,\AC^平面POD,而ACÌ平面PAC,
\平面POD^平面PAC 5分
(2)在平面POD中,过O作OH^PD于H,由(1)知:
平面POD^平面PAC,\OH^平面PAC,过H作HG^PA于G,连OG,则OG^PA(三垂线定理)
\ÐOGH为二面角B—PA—C的平面角,
在RtDODA中,OD=OA×450=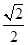 .
.
在RtDPOD中,OH= 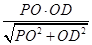 =
=  =
=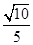 .
.
在RtDPOA中,OG= 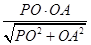 =
= 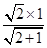 =
=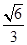 .
.
在RtDOHG中,sinÐOGH= 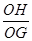 =
= 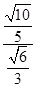 =
=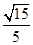 .
.
所以,cosÐOGH= 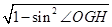 =
= 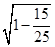 =
=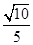
所以,二面角B—PA—C的余弦值为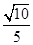 . 10分
. 10分
考点:1.平面与平面垂直的判定;2.二面角的平面角作法与求法


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com