Question

17．如图所示是正三棱锥V-ABC的正视图，侧视图和俯视图，则其正视图的面积为（　　）  

• A． 6
• B． 5
• C． 4$\sqrt{3}$
• D． 3$\sqrt{3}$

Answer 1

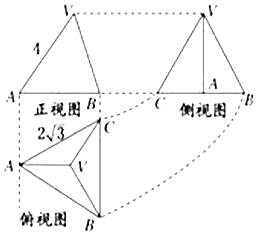
分析 由三视图求出正三棱锥的棱长、底面正三角形的边长，根据正三棱锥的结构特征求出三棱锥的高，即可求出正视图的面积．

解答 解：由题意知几何体是一个正三棱锥，
由三视图得棱长为4，底面正三角形的边长为2$\sqrt{3}$，
∴底面正三角形的高是$\sqrt{12-3}$=3，
∵正三棱锥顶点在底面的射影是底面的中心，
∴正三棱锥的高h=2$\sqrt{3}$，
∴正视图的面积S=$\frac{1}{2}×\frac{\sqrt{3}}{2}×2\sqrt{3}×2\sqrt{3}$=3$\sqrt{3}$，
故选：D．

点评 本题考查正三棱锥的三视图，由三视图正确求出几何元素的长度是解题的关键，考查了空间想象能力．