
 某高校自主招生考试中,所有去面试的考生全部参加了“语言表达能力”和“竞争与团队意识”两个科目的测试,成绩分别为A、B、C、D、E五个等级,某考场考生的两科测试成绩数据统计如图,其中“语言表达能力”成绩等级为B的考生有10人.
某高校自主招生考试中,所有去面试的考生全部参加了“语言表达能力”和“竞争与团队意识”两个科目的测试,成绩分别为A、B、C、D、E五个等级,某考场考生的两科测试成绩数据统计如图,其中“语言表达能力”成绩等级为B的考生有10人.| 40(1×0.2+2×0.1+3×0.375+4×0.25+5×0.075) |
| 40 |
| ||
|
| 1 |
| 3 |
| ||||
|
| 4 |
| 15 |
| ||||||
|
| 13 |
| 45 |
| ||||
|
| 4 |
| 45 |
| ||
|
| 1 |
| 45 |
| X | 16 | 17 | 18 | 19 | 20 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 3 |
| 4 |
| 15 |
| 13 |
| 45 |
| 4 |
| 45 |
| 1 |
| 45 |
| 86 |
| 5 |
| 86 |
| 5 |


科目:高中数学 来源: 题型:
| x |
| x-1 |
|
| sinx |
| x |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{x|0<x<1} |
| B、{x|1≤x<2} |
| C、{x|1<x<2} |
| D、{x|0<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
| OQ |
| OA |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
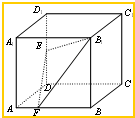
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 省份 | 四川 | 河南 | 湖北 | 安徽 |
| 人数 | 45 | 60 | 30 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com