
 已知抛物线C:x2=4y,F为抛物线焦点,圆E:x2+(y+1)2=1,斜率为k(k>0)的直线l与抛物线C和圆E都相切,切点分别为P和Q,直线PF和PQ分别交x轴于点M,N.
已知抛物线C:x2=4y,F为抛物线焦点,圆E:x2+(y+1)2=1,斜率为k(k>0)的直线l与抛物线C和圆E都相切,切点分别为P和Q,直线PF和PQ分别交x轴于点M,N.分析 (Ⅰ)设直线y=kx+t(k>0,t<0),代入抛物线的方程,运用判别式为0,求得k,t的关系式;再将直线和圆相切的条件:d=r,解得k,t,进而得到直线l的方程;
(Ⅱ)将直线l的方程代入抛物线的方程可得P的坐标,由直线PF求得M的坐标,直线的方程求得N的坐标,再运用三角形的面积公式和等积法,计算即可得到所求值.
解答 解:(Ⅰ)设直线y=kx+t(k>0,t<0),
代入抛物线的方程x2=4y,可得x2-4kx-4t=0,
由相切的条件可得△=16k2+16t=0,即为k2+t=0,
由直线和圆相切可得d=$\frac{|t+1|}{\sqrt{1+{k}^{2}}}$=1,
即为t2+3t=0,解得t=-3(0舍去),
k=$\sqrt{3}$,(负的舍去),
即有直线l的方程为y=$\sqrt{3}$x-3;
(Ⅱ)由y=$\sqrt{3}$x-3和x2=4y,
解得切点P(2$\sqrt{3}$,3),
由F(0,1),直线PF的方程为y=$\frac{\sqrt{3}}{3}$x+1,
求得M的坐标为(-$\sqrt{3}$,0);
直线l的方程为y=$\sqrt{3}$x-3,可得N的坐标为($\sqrt{3}$,0),
由面积相等法,可得S△PMN=$\frac{1}{2}$•2$\sqrt{3}$•3=3$\sqrt{3}$,
又设内切圆的半径为r,可得$\frac{1}{2}$r(|PM|+|PN|+|MN|)=$\frac{1}{2}$r(6+2$\sqrt{3}$+2$\sqrt{3}$),
即有(3+2$\sqrt{3}$)r=3$\sqrt{3}$,
解得r=6-3$\sqrt{3}$.
则△PMN内切圆半径为6-3$\sqrt{3}$.
点评 本题考查直线和抛物线相切、以及直线与圆相切的条件,考查等积法的运用以及内切圆半径的求法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 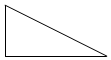 | B. | 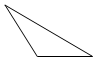 | C. | 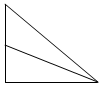 | D. | 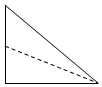 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 11 |
| A. | 23个 | B. | 24个 | C. | 25个 | D. | 26个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
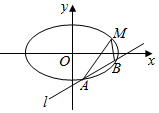 ⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.
⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com