
| A. | 2 | B. | 4 | C. | 2i | D. | 4i |
分析 复数z=1+ai(a∈R)在复平面对应的点在第一象限,可得a>0,$\overline{z}$=1-ai.由|$\overrightarrow{z}$|=$\sqrt{5}$,可得$\sqrt{1+{a}^{2}}$=$\sqrt{5}$,解得a.
解答 解:复数z=1+ai(a∈R)在复平面对应的点在第一象限,∴a>0,$\overline{z}$=1-ai.
∵|$\overrightarrow{z}$|=$\sqrt{5}$,∴$\sqrt{1+{a}^{2}}$=$\sqrt{5}$,解得a=2.
则z的虚部为2.
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 90° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 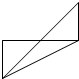 | C. | 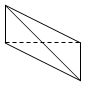 | D. | 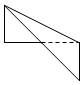 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 项目 | 收案(件) | 结案(件) | |
| 判决(件) | ||||
| 1 | 刑事案件 | 2400 | 2400 | 2400 |
| 2 | 婚姻家庭、继承纠纷案件 | 3000 | 2900 | 1200 |
| 3 | 权属、侵权纠纷案件 | 4100 | 4000 | 2000 |
| 4 | 合同纠纷案件 | 14000 | 13000 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,6] | B. | [6,+∞) | C. | (-∞,-4] | D. | [-4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | (-∞,-1)∪[2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com