
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)已知![]() 在定义域上为减函数,若对任意的
在定义域上为减函数,若对任意的![]() ,不等式
,不等式![]() 为常数)恒成立,求
为常数)恒成立,求![]() 的取值范围.
的取值范围.
【答案】解:(1)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,
=0,
即![]() ………………………3
………………………3
(2)由(1)知![]() ,………………………5
,………………………5
设![]()
![]() ,则
,则![]() .
.
因为函数y=2![]() 在R上是增函数且
在R上是增函数且![]() , ∴
, ∴![]() >0.
>0.
又![]() >0 ,∴
>0 ,∴![]() >0,即
>0,即![]() ,
,
∴![]() 在
在![]() 上为减函数.另法:或证明f′(x)
上为减函数.另法:或证明f′(x)![]() 0………………………9
0………………………9
(3)因为![]() 是奇函数,从而不等式
是奇函数,从而不等式
![]() 等价于
等价于![]() ,………………………3
,………………………3
因为![]() 为减函数,由上式推得
为减函数,由上式推得![]() .即对一切
.即对一切![]() 有
有![]() ,
,
从而判别式![]() ………………………13
………………………13
【解析】
定义域为R的奇函数![]() ,得b=1,在代入1,-1,函数值相反得a;
,得b=1,在代入1,-1,函数值相反得a;
![]()
![]() ,通常用函数的单调性转化为自变量的大小关系。
,通常用函数的单调性转化为自变量的大小关系。
(1)![]()
![]() 是奇函数,
是奇函数,![]()
![]() ,┈┈┈┈┈┈┈┈┈┈┈┈2分
,┈┈┈┈┈┈┈┈┈┈┈┈2分
即![]()
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
(2)由(1)知![]()
由上式易知![]() 在R上为减函数。 ┈┈┈┈┈┈┈┈┈┈┈┈2分
在R上为减函数。 ┈┈┈┈┈┈┈┈┈┈┈┈2分
又因为![]() 为奇函数,从而不等式
为奇函数,从而不等式![]() ,
,
等价于![]() ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分
![]()
![]() 为减函数
为减函数![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
即对一切![]() 都有
都有![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分
![]()
![]()
![]()
![]() ┈┈┈┈┈┈┈┈┈┈┈┈1分
┈┈┈┈┈┈┈┈┈┈┈┈1分


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的一条准线方程为x=
(a>b>0)的一条准线方程为x=![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
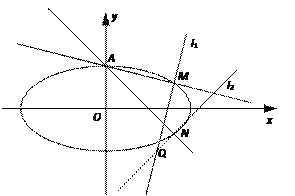
(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.
① 设直线AM,AN的斜率分别是k1, k2,求k1k2的值;
② 过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜
(单位:千克)清洗该蔬菜![]() 千克后,蔬菜上残留的农药
千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

在坐标系中描出散点图,并判断变量![]() 与
与![]() 的相关性;
的相关性;

(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 和
和![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() 精确到0.1)
精确到0.1)

(3)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )(附:线性回归方程计算公式:
)(附:线性回归方程计算公式:  ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量![]() 单位:克
单位:克![]() ,重量分组区间为
,重量分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,由此得到样本的重量频率分布直方图
,由此得到样本的重量频率分布直方图![]() 如图
如图![]() .
.
(1)求![]() 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取3个小球,其中重量![]() 内的小球个数为
内的小球个数为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是
是![]() 的中点,
的中点, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.

(![]() )求证
)求证![]() .
.
(![]() )若点
)若点![]() 是平面
是平面![]() 内一动点,且
内一动点,且![]() ,请在平面
,请在平面![]() 内,建立适当的坐标系,求出点
内,建立适当的坐标系,求出点![]() 的轨迹方程,并求出点
的轨迹方程,并求出点![]() 在
在![]() 内的轨迹长度.
内的轨迹长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com