
分析 把函数y=$\sqrt{(2-a){x}^{2}-2(a-2)x+4}$的定义域为R转化为(2-a)x2-2(a-2)x+4≥0对任意x∈R恒成立.然后分a=2和a≠2分类求解得答案.
解答 解:∵y=$\sqrt{(2-a){x}^{2}-2(a-2)x+4}$的定义域为R,
∴(2-a)x2-2(a-2)x+4≥0对任意x∈R恒成立.
当a=2时,不等式化为4≥0恒成立;
当a≠2时,需$\left\{\begin{array}{l}{2-a>0}\\{△=4(a-2)^{2}-16(2-a)≤0}\end{array}\right.$,解得-2≤a<2.
综上,-2≤a≤2.
∴实数a的取值范围为[-2,2].
故答案为:[-2,2].
点评 本题考查函数定义域及其求法,考查数学转化思想方法,体现了分类讨论的数学思想方法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
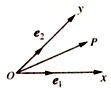 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com