
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由已知得M点的轨迹是以原点O为圆心,半焦距c为半径的圆,该圆内含于椭圆,由此能求出椭圆离心率的取值范围.
解答 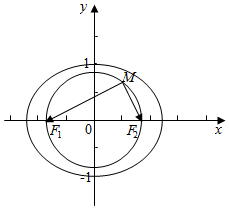 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),得F1(-c,0),F2(c,0)
解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),得F1(-c,0),F2(c,0)
∵MF1⊥MF2,
∴M点的轨迹是以原点O为圆心,半焦距c为半径的圆.
又∵M点总在椭圆内部,
∴该圆内含于椭圆,可得c<b,
平方得c2<b2,即c2<a2-c2.
∴e2=$\frac{{c}^{2}}{{a}^{2}}$<$\frac{1}{2}$,可得离心率e满足:0<e<$\frac{\sqrt{2}}{2}$.
∴椭圆离心率的取值范围是(0,$\frac{\sqrt{2}}{2}$).
故答案为:(0,$\frac{\sqrt{2}}{2}$).
点评 本题考查椭圆的离心率的取值范围的求法,是中档题,解题时要认真审题,注意椭圆、圆的性质的合理运用.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A∪B=R | C. | A∩(∁RB)=∅ | D. | B∩(∁RA)=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com