练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知点F1（-$\sqrt{13}$，0）和点F2（$\sqrt{13}$，0）是椭圆E的两个焦点，且点A（0，6）在椭圆E上．
    （1）求椭圆E的方程；
    （2）设P是椭圆E上的一点，若|PF2|=4，求以线段PF1为直径的圆的面积．

    分析 （1）由椭圆的焦点坐标结合椭圆过定点可求椭圆的长轴长，再由隐含条件求得b2，则椭圆方程可求；
    （2）由椭圆定义结合已知求得|PF1|，再由圆的面积公式得答案．

    解答 解：（1）∵椭圆的两个焦点F1（-$\sqrt{13}$，0），F2（$\sqrt{13}$，0），且点A（0，6）在椭圆E上，
    ∴$2a=\sqrt{（-\sqrt{13}-0）^{2}+（0-6）^{2}}+\sqrt{（\sqrt{13}-0）^{2}+（0-6）^{2}}$=14，
    则a=7，∴b2=a2-c2=49-13=36，
    则椭圆方程为：$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{36}=1$；
    （2）由|PF2|=4，得|PF1|=2a-|PF2|=14-4=10，
    ∴以线段PF1为直径的圆的面积为π•52=25π．

    点评 本题考查椭圆的简单性质，考查了由题意的定义求椭圆的方程，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2，E，F分别是AB，AD的中点，则点C到平面GEF的距离为$\frac{6\sqrt{11}}{11}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以原点为圆心、椭圆的短半轴长为半径的⊙E与直线x-y+$\sqrt{6}$=0相切．
    （1）求椭圆C的方程；
    （2）过定点Q（1，0）斜率为k的直线与椭圆C交于M，N两点，若$\overrightarrow{OM}$$•\overrightarrow{ON}$=-2，求斜率k的值；
    （3）若（2）中的直线MN与⊙E交于A，B两点，设点P在⊙E上．试探究使△PAB的面积为$\frac{\sqrt{21}}{12}$的点P共有几个？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在平面直角坐标系xOy中，以原点为极点，以x轴正半轴为极轴建立极坐标系，已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=2+2sinα}\end{array}\right.$（α为参数），曲线C2的方程为x2+（y-4）2=16．
    （Ⅰ）求曲线C1的极坐标方程；
    （Ⅱ）若曲线θ=$\frac{π}{3}$（ρ＞0）与曲线C1．C2交于A，B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，且经过点（$\sqrt{2}$，$\frac{\sqrt{3}}{3}$）．
    （1）求椭圆的标准方程；
    （2）若直线1经过点F（$\sqrt{2}$，0）与直线x=$\frac{3\sqrt{2}}{2}$交于点M，与椭圆交于A，B两点，设P为直线x=$\sqrt{2}$上异于F的点，设PA，PB，PM的斜率分别为k1，k2，k3，求证：k1+k2=2k3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在直角坐标系xOy中，直线l过点M（3，4），其倾斜角为45°，圆C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}\right.（θ为参数）$．再以原点为极点，以x正半轴为极轴建立极坐标系，并使得它与直角坐标系xoy有相同的长度单位．
    （1）求圆C的极坐标方程；
    （2）设圆C与直线l交于点A、B，求|MA|•|MB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图，在平行六面体ABCD-A1B1C1D1中，AC与BD的交点为点M．设$\overrightarrow{{C_1}{D_1}}=\overrightarrow a$，$\overrightarrow{{C_1}{B_1}}=\overrightarrow b$，$\overrightarrow{{C_1}C}=\overrightarrow c$，用$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$表示向量$\overrightarrow{M{B_1}}$，则$\overrightarrow{M{B}_{1}}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{c}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

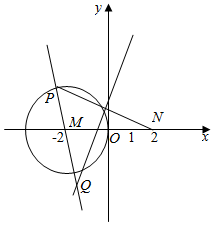    17．已知P为圆M：（x+2）2+y2=4上的动点，N（2，0），线段PN的垂直平分线与直线PM的交点为Q，点Q的轨迹方程为x2-$\frac{{y}^{2}}{3}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，椭圆的左、右焦点分别是F1、F2，点M为椭圆上的一个动点，△MF1F2面积的最大值为$\sqrt{3}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）P为椭圆上一点，PF1与y轴相交于Q，且$\overrightarrow{{F}_{1}P}$=2$\overrightarrow{{F}_{1}Q}$．若PF1与椭圆相交于另一点R，求△PRF2的面积．

    查看答案和解析>>

    同步练习册答案