
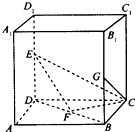
 如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.分析 (1)建立如图所示的空间直有坐标系求解$\overrightarrow{EF}$=($\frac{1}{2}$,$\frac{1}{2}$,-$\frac{1}{2}$),$\overrightarrow{CF}$=($\frac{1}{2}$,-$\frac{1}{2}$,0),运用数量积证明即可.
(2)运用公式COS<$\overrightarrow{EF}$,$\overrightarrow{CG}$>=$\frac{\overrightarrow{EF}•\overrightarrow{CG}}{|\overrightarrow{EF}|•|\overrightarrow{CG}|}$=,求解夹角即可.
解答 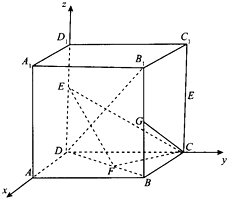 (1)证明:建立如图所示的空间直有坐标系D-xyz,(1分)
(1)证明:建立如图所示的空间直有坐标系D-xyz,(1分)
则D(0,0,0),E(0,0,$\frac{1}{2}$),C(0,1,0),F($\frac{1}{2}$,$\frac{1}{2}$,0),G(1,1,$\frac{1}{2}$)
所以$\overrightarrow{EF}$=($\frac{1}{2}$,$\frac{1}{2}$,-$\frac{1}{2}$),$\overrightarrow{CF}$=($\frac{1}{2}$,-$\frac{1}{2}$,0),
$\overrightarrow{CG}$=(1,0,$\frac{1}{2}$),
$\overrightarrow{CE}$=(0,-1,$\frac{1}{2}$).(4分) 因为$\overrightarrow{EF}$$•\overrightarrow{CF}$=$\frac{1}{2}×\frac{1}{2}$$+\frac{1}{2}×$(-$\frac{1}{2}$)+(-$\frac{1}{2}$)×0=0,
所以$\overrightarrow{EF}$⊥$\overrightarrow{CF}$,
即EF⊥CF.
(2)解:因为$\overrightarrow{EF}$$•\overrightarrow{CF}$=$\frac{1}{2}×1$$+\frac{1}{2}×0$+(-$\frac{1}{2}$)×$\frac{1}{2}$=$\frac{1}{4}$
|$\overrightarrow{EF}$|=$\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$
$\overrightarrow{CG}$|=$\sqrt{{1}^{2}+{0}^{2}+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$
所以COS<$\overrightarrow{EF}$,$\overrightarrow{CG}$>=$\frac{\overrightarrow{EF}•\overrightarrow{CG}}{|\overrightarrow{EF}|•|\overrightarrow{CG}|}$=$\frac{\frac{1}{4}}{\frac{\sqrt{3}}{2}•\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{15}}{15}$
点评 本题考察了运用空间坐标系解决空间直线的位置关系,解决空间直线的夹角问题,属于中档题,关键是准确求解坐标,计算长度,数量积.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份 | 一月 | 二月 | 三月 | 四月 |
| 交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sinx-cosx | B. | cosx-sinx | C. | sinx-cosx | D. | sinx+cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+2y-12=0 | B. | 2x+3y-13=0 | C. | 3x-2y=0 | D. | 2x-3y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}}]$ | B. | $[{\frac{1}{2},1})$ | C. | $({0,\frac{{\sqrt{3}}}{2}}]$ | D. | $[{\frac{{\sqrt{3}}}{2},1})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com