
分析 (1)求出函数的解析式,然后求解函数的最大值,通过|m-1|≤1,求解m的范围,得到m的最大值M.
(2)利用分析法,证明不等式成立的充分条件即可.
解答 解:(1)由已知可得f(x)=$\left\{\begin{array}{l}{-1,x<0}\\{2x-1,0≤x≤1}\\{1,x>1}\end{array}\right.$,
所以fmax(x)=1,…(3分)
所以只需|m-1|≤1,解得-1≤m-1≤1,∴0≤m≤2,
所以实数m的最大值M=2…(5分)
(2)因为a>0,b>0,
所以要证a+b≥2ab,只需证(a+b)2≥4a2b2,
即证a2+b2+2ab≥4a2b2,
所以只要证2+2ab≥4a2b2,…(7分)
即证2(ab)2-ab-1≤0,
即证(2ab+1)(ab-1)≤0,因为2ab+1>0,所以只需证ab≤1,
下证ab≤1,
因为2=a2+b2≥2ab,所以ab≤1成立,
所以a+b≥2ab…(10分)
点评 本题考查函数的最值的求法,基本不等式的应用,考查分析法的应用,考查逻辑推理能力以及计算能力.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=-|x-1| | B. | y=x2-2x+3 | C. | y=ln(x+1) | D. | y=2${\;}^{-\frac{x}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
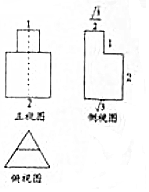 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{9\sqrt{3}}}{4}$ | C. | $3\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
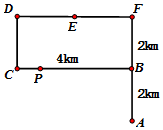 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com