
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m⊥β,则α∥β | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m⊥α,α∩β=n,则m∥n |
分析 在A中,由直线与平面垂直的判定定理得n⊥α;在B中,由面面平行的判定定理得α∥β;在C中,由面面垂直的判定定理得α⊥β;在D中,m与n相交、平行或异面.
解答 解:由α、β是两个平面,m、n是两条直线,知:
在A中:若m∥n,m⊥α,则由直线与平面垂直的判定定理得n⊥α,故A正确;
在B中:若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故B正确;
在C中:若m⊥α,m?β,则由面面垂直的判定定理得α⊥β,故C正确;
在D中:若m⊥α,α∩β=n,则m与n相交、平行或异面,故D错误.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [0,$\frac{2}{3}$] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-2i | B. | -$\frac{1}{2}$+i | C. | -$\frac{1}{2}$-i | D. | $\frac{1}{2}$-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
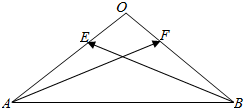 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 280 | B. | 35 | C. | -35 | D. | -280 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com