
分析 (1)使用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{PQ},\overrightarrow{PG}$,根据P,Q,G三点共线得出λ,μ的关系;
(2)用λ表示出μ,令λ,μ∈(0,1)得出λ的范围,则λμ可表示为关于λ的函数,求出该函数的最值即可.
解答 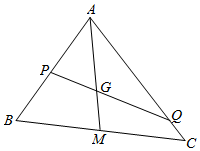 解:(1)连结AG并延长交BC于M,则M是BC的中点,则$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$.
解:(1)连结AG并延长交BC于M,则M是BC的中点,则$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$.
又$\overrightarrow{AP}=λ\overrightarrow{AB}$,$\overrightarrow{AQ}=μ\overrightarrow{AC}$,
∴$\overrightarrow{PQ}=\overrightarrow{AQ}-\overrightarrow{AP}$=$μ\overrightarrow{AC}-λ\overrightarrow{AB}$,$\overrightarrow{PG}=\overrightarrow{AG}-\overrightarrow{AP}$=($\frac{1}{3}-λ$)$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$.
∵P,G,Q三点共线,故存在实数t,使$\overrightarrow{PG}$=t$\overrightarrow{PQ}$,即($\frac{1}{3}-λ$)$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$=$μt\overrightarrow{AC}-λt\overrightarrow{AB}$.
∴$\left\{\begin{array}{l}{\frac{1}{3}-λ=-λt}\\{\frac{1}{3}=μt}\end{array}\right.$,两式相除消去t得1-3λ=-$\frac{λ}{μ}$,即$\frac{1}{λ}+\frac{1}{μ}=3$.
(2)∵1-3λ=-$\frac{λ}{μ}$,∴$μ=\frac{λ}{3λ-1}$,
∵λ,μ∈(0,1),∴$\left\{\begin{array}{l}{0<λ<1}\\{0<\frac{λ}{3λ-1}<1}\end{array}\right.$,解得$\frac{1}{2}<λ<1$.∴$1<\frac{1}{λ}<2$.
∴λμ=$\frac{{λ}^{2}}{3λ-1}$=$\frac{1}{\frac{3}{λ}-\frac{1}{{λ}^{2}}}=\frac{1}{-(\frac{1}{λ}-\frac{3}{2})^{2}+\frac{9}{4}}$.
∴当$\frac{1}{λ}=\frac{3}{2}$时,λμ取得最小值$\frac{4}{9}$,当$\frac{1}{λ}=1$或2时,λμ取得最大值$\frac{1}{2}$.
∴λμ的取值范围是[$\frac{4}{9}$,$\frac{1}{2}$).
点评 本题考查了平面向量的基本定理,不等式的解法,根据图形寻找向量的关系是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
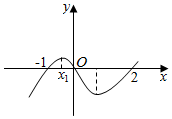
| A. | (-∞,-2) | B. | (-∞,-1) | C. | (-3,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,0) | B. | [-6,0] | C. | (-1,0] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com