科目：高中数学 来源： 题型：解答题
某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价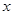
（元/件），可近似看做一次函数
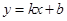的关系（图象如下图所示）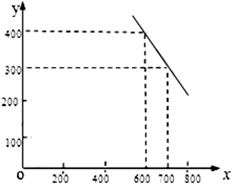
（1）根据图象，求一次函数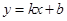的表达式；
（2）设公司获得的毛利润为S元,
①求S关于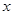的函数表达式；
②求该公司可获得的最大毛利润，并求出此时相应的销售单价．
（提示：毛利润＝销售总价－成本总价）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在
上是减函数，求函数
在
上的最大值与最小值．
时，
，
=
；
时，
．
对于任意的
满足
.
的值；
为偶函数；
上是增函数，解不等式
．
的图象为曲线
，若存在实数
，使得曲线
处有斜率是
的切线，求实数
的取值范围；
，且
时，证明：
.
在区间
上的最大值为2，求实数a的值．
对于任意
, 总有
，
，
上的单调递增函数
，求解不等式
在
上为增函数，求正实数
的取值范围；
，求证：
，
时，求
的值；
在
上是减函数，并求函数的最大值和最小值．
在
上是减函数，求不等式
的解集。