分析：根据三角形外接圆的性质，结合|
|=|
|=|
|，可得O为△ABC的外心；根据向量加法的平行四边形法则和向量共线定理，可证出N为△ABC的三条中线的交点，得N为△ABC的重心；根据向量数量积的运算性质与向量减法法则，结合
•
=
•
，证出
⊥，点P在AC边上的高所在直线上．同理可得点P也在AB、BC边上的高所在直线上，因此，P是△ABC三条高所在直线的交点，即得P为△ABC的垂心．
解答：
解：①若|
|=|
|=|
|，则点O到A、B、C三点的距离相等，
∴O为△ABC的外接圆的圆心，即外心；
②若
+
+
=
，则
+
=-
，
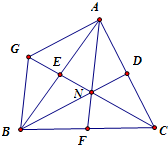
以NA、NB为邻边作平行四边形NAGB，
可得GN、AB的交点E为AB的中点，且E、N、C三点共线．
因此，CE为△ABC的中线．同理可得BN、AN也在△ABC的中线上．
∴点N为△ABC的三条中线的交点，可得N为△ABC的重心；
③若
•
=
•
，
可得（
-
）•
=0，
∴
•=0，可得
⊥，点P在AC边上的高所在直线上．
同理可得点P也在AB、BC边上的高所在直线上．
因此，P是△ABC三条高所在直线的交点，即得P为△ABC的垂心．
综上所述，点O、N、P依次是△ABC的外心、重心、垂心．
故答案为：外心、重心、垂心
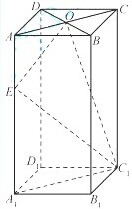如图，长方体ABCD-A1B1C1D1中，底面A1B1C1D1是正方形，E为棱AA1上任意一点，F是CD的中点．
在棱长为2的正方体ABCD-A1B1C1D1中，E为棱AB的中点，点P在平面A1B1C1D1内，若D1P⊥平面PCE，试求线段D1P的长．