
【题目】已知动圆P经过点![]() ,并且与圆
,并且与圆![]() 相切.
相切.
(Ⅰ)求圆心P的轨迹C的方程;
(Ⅱ)O是坐标原点,过点![]() 的直线
的直线![]() 与C交于A,B两点,在C上是否存在点Q,使得四边形
与C交于A,B两点,在C上是否存在点Q,使得四边形![]() 是平行四边形?
是平行四边形?
【答案】(1) ![]() ;
;
(2) 直线![]() 为
为![]() 或
或![]() 时,椭圆C上存在点Q,否则不存在.
时,椭圆C上存在点Q,否则不存在.
【解析】
(1) 由椭圆的定义可得,P的轨迹是以M,N为焦点的椭圆,进而求出方程.
(2) 假设存在,根据平行四边形已知三个点坐标,表示Q的坐标,设直线方程,联立直线和椭圆方程,利用韦达定理整理Q的坐标,根据Q在椭圆上,求得直线方程.
(1) 由题意可得N在圆M内部,所以两圆内切,
所以![]() ,
,
由椭圆的定义可知,点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
设椭圆方程为![]() ,
,
其中![]() ,
,![]() ,
,
所以![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2) 假设C上存在点Q,使得四边形![]() 是平行四边形,
是平行四边形,
由题意可知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]()
设直线![]() 与椭圆C的交点
与椭圆C的交点![]() ,
,
则![]()
联立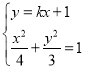 可得,
可得,![]()
由韦达定理可得,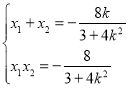
![]()
所以![]() ,
,
点 Q在椭圆C上,所以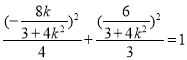 ,
,
解得![]()
综上可得,直线![]() 为
为![]() 或
或![]() 时,
时,
椭圆C上存在点Q,使得四边形![]() 是平行四边形,否则不存在.
是平行四边形,否则不存在.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为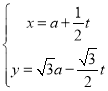 (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点、
).在以坐标原点为极点、![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式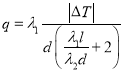 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
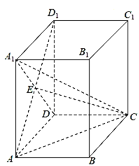
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 中,棱
中,棱![]() ,
,![]() 所在直线所成角为
所在直线所成角为![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,当四面体
,当四面体![]() 的体积取得最大值时( ).
的体积取得最大值时( ).
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.
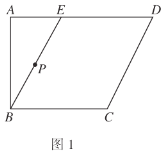
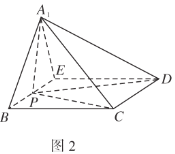
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,当直线
上,当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日,武汉市雷神山医院为确诊新型冠状病毒肺炎患者,需要检测核酸是否为阳性,现有![]() 份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测
份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测![]() 次;(2)混合检测,将其中
次;(2)混合检测,将其中![]() (
(![]() ,且
,且![]() )份核酸样本分别取样混合在一起检测,若检测结果为阴性,这
)份核酸样本分别取样混合在一起检测,若检测结果为阴性,这![]() 份核酸样本全为阴性,因而这
份核酸样本全为阴性,因而这![]() 份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这
份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这![]() 份核酸样本究竟哪几份为阳性,就要对这
份核酸样本究竟哪几份为阳性,就要对这![]() 份样本再逐份检测,此时这
份样本再逐份检测,此时这![]() 份核酸样本的检测次数总共为
份核酸样本的检测次数总共为![]() 次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份核酸样本,其中只有2份样本为阳性,若采用逐份检测方式,求恰好经过4次检测就能把阳性样本全部检测出来的概率.
(2)现取其中![]() (
(![]() ,且
,且![]() )份核酸样本,记采用逐份检测方式,样本需要检测的总次数为
)份核酸样本,记采用逐份检测方式,样本需要检测的总次数为![]() ,采用混合检测方式,样本需要检测的总次数为
,采用混合检测方式,样本需要检测的总次数为![]() .
.
①试运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求
,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() 年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数
年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数![]() 和平均温度
和平均温度![]() 有关,现收集了以往某地的
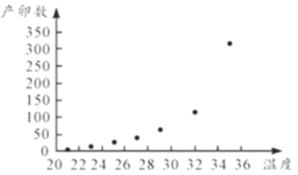
有关,现收集了以往某地的![]() 组数据,得到下面的散点图及一些统计量的值.
组数据,得到下面的散点图及一些统计量的值.
平均温度 |
|
|
|
|
|
|
|
平均产卵数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数![]() 关于平均温度
关于平均温度![]() 的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出![]() 关于
关于![]() 的回归方程.(结果精确到小数点后第三位)
的回归方程.(结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到![]() 以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到
以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到![]() 以上的概率为
以上的概率为![]() .
.
①记该地今后![]() 年中,恰好需要
年中,恰好需要![]() 次人工防治的概率为
次人工防治的概率为![]() ,求
,求![]() 取得最大值时相应的概率
取得最大值时相应的概率![]() ;
;
②根据①中的结论,当![]() 取最大值时,记该地今后
取最大值时,记该地今后![]() 年中,需要人工防治的次数为
年中,需要人工防治的次数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数1-9的一种方法.例如:3可表示为“≡”,26可表示为“=⊥”,现有6根算筹,据此表示方法,若算筹不能剩余,则可以用1-9这9个数字表示两位数中,能被3整除的概率是( )
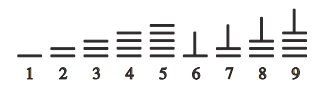
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com