
分析 由题意可得f(x)的图象关于直线x=$\frac{π}{4}$对称,f($\frac{π}{4}$)=sin($\frac{π}{4}$ω+$\frac{π}{2}$)=-1,即即ω=8k-4;再结合$\frac{π}{3}$-$\frac{π}{4}$<$\frac{T}{2}$=$\frac{π}{ω}$,求得ω的值.
解答 解:由f($\frac{π}{6}$)=f($\frac{π}{3}$),可得f(x)的图象关于直线x=$\frac{\frac{π}{6}+\frac{π}{3}}{2}$=$\frac{π}{4}$对称.
再根据f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上有最小值,可得f($\frac{π}{4}$)=sin($\frac{π}{4}$ω+$\frac{π}{2}$)=-1,
∴$\frac{π}{4}$ω+$\frac{π}{2}$=2kπ-$\frac{π}{2}$,k∈z,即ω=8k-4,k∈z.
再根据f(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上无最大值,$\frac{π}{3}$-$\frac{π}{4}$<$\frac{T}{2}$=$\frac{π}{ω}$,求得ω<12.
综合可得ω=4,
故答案为:4.
点评 本题主要考查正弦函数的图象特征,正弦函数的图象的对称性、定义域和值域,属于基础题.


科目:高中数学 来源: 题型:解答题
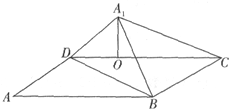 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com