
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中: 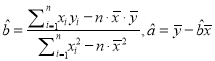 ,
, ![]() ,
, ![]()
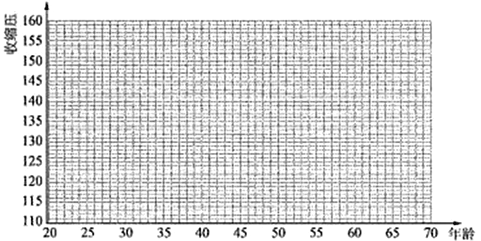
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
【答案】(1)答案见解析;(2) ![]() ;(3)中度高血压人群.
;(3)中度高血压人群.
【解析】试题分析:(1)将数据对应描点,即得散点图,(2)先求均值,再代人公式求![]() ,利用
,利用![]() 求
求![]() ,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
试题解析:(1) 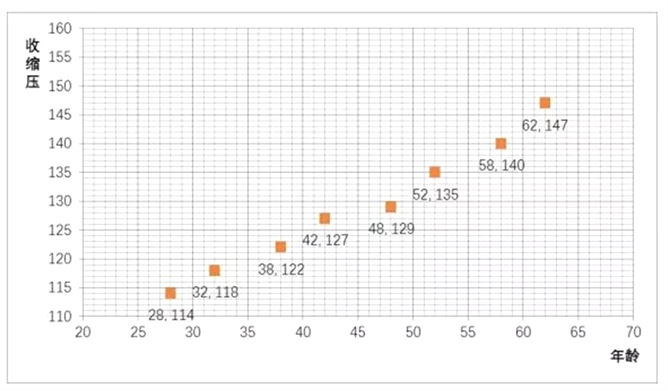
(2)![]()
![]()
∴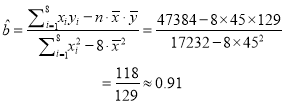
![]()
∴回归直线方程为![]() .
.
(3)根据回归直线方程的预测,年龄为70岁的老人标准收缩压约为![]() (mmHg)∵
(mmHg)∵![]()
∴收缩压为180mmHg的70岁老人为中度高血压人群.
【题型】解答题
【结束】
19
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)设![]() 为
为![]() 的中点,根据平几知识可得四边形
的中点,根据平几知识可得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面
,再根据线面平行判定定理得结论,(2)根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面![]() 一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得
一个法向量,根据向量数量积求向量夹角,再根据线面角与向量夹角互余关系列等式,解得![]() 的长.
的长.
试题解析:(1)证明:设![]() 为
为![]() 的中点,连
的中点,连![]()
因为![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]()
![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为![]() 是菱形,且
是菱形,且![]() ,
,
所以![]() 是等边三角形
是等边三角形
取![]() 中点
中点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
, ![]()
建立如图的空间直角坐标系,令![]() ,
,
则![]() ,
, 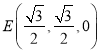 ,
, ![]() ,
, ![]() ,
,
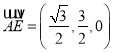 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() 且
且![]() ,
,
取![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则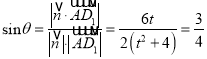 ,
,
解得![]() ,故线段
,故线段![]() 的长为2.
的长为2.


科目:高中数学 来源: 题型:
【题目】过原点的一条直线与椭圆![]() =1(a>b>0)交于A,B两点,以线段AB为直径的圆过该椭圆的右焦点F2,若∠ABF2∈[
=1(a>b>0)交于A,B两点,以线段AB为直径的圆过该椭圆的右焦点F2,若∠ABF2∈[![]() ],则该椭圆离心率的取值范围为( )
],则该椭圆离心率的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中正确的是( )
是两个不同的平面,则下列命题中正确的是( )
A. 若![]() ,
, ![]() ,则
,则![]()
B. 若![]() ,
, ![]() ,则
,则![]()
C. 若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,则
,则![]()
【答案】C
【解析】A. 若![]() ,
, ![]() ,则
,则![]() 或
或![]() ;
;
B. 若![]() ,
, ![]() ,则
,则![]() 无交点,即平行或异面;
无交点,即平行或异面;
C. 若![]() ,
, ![]() ,
, ![]() ,过
,过![]() 作平面与
作平面与![]() 分别交于直线s,t,则
分别交于直线s,t,则![]() ,
, ![]() ,所以
,所以![]() t,再根据线面平行判定定理得
t,再根据线面平行判定定理得![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() ,即
,即![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,当B在平面
,当B在平面![]() 内时才有
内时才有![]() ,
,
综上选C.
【题型】单选题
【结束】
11
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)![]() Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
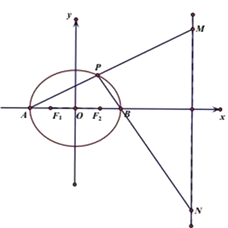
【题目】椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,若椭圆过点
,若椭圆过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
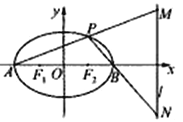
(2)若![]() 为椭圆的左、右顶点,
为椭圆的左、右顶点, ![]() (
(![]() )为椭圆上一动点,设直线
)为椭圆上一动点,设直线![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() ,判断线段
,判断线段![]() 为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
为直径的圆是否经过定点,若是,求出该定点坐标;若不恒过定点,说明理由.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)将点坐标代人椭圆方程 并与离心率联立方程组,解得![]() ,
, ![]() (2)根据点斜式得直线
(2)根据点斜式得直线![]() 方程,与直线
方程,与直线![]() 联立解得点
联立解得点![]() 坐标,根据向量关系得
坐标,根据向量关系得![]() 为直径的圆方程,最后代人椭圆方程进行化简,并根据恒等式成立条件求定点坐标.
为直径的圆方程,最后代人椭圆方程进行化简,并根据恒等式成立条件求定点坐标.
试题解析:(1)由已知![]() ,
,
∴![]() ①
①
∵椭圆过点![]() ,
,
∴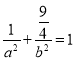 ②
②
联立①②得![]() ,
, ![]()
∴椭圆方程为![]()
(2)设![]() ,已知
,已知![]()
∵![]() ,∴
,∴![]()
∴![]() 都有斜率
都有斜率
∴![]()
∴![]() ③
③
∵![]()
∴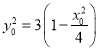 ④
④
将④代入③得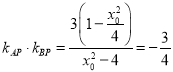
设![]() 方程
方程![]()
∴![]() 方程
方程![]()
∴![]()
由对称性可知,若存在定点,则该定点必在![]() 轴上,设该定点为
轴上,设该定点为![]()
则![]()
∴![]()
∴![]() ,∴
,∴![]()
∴存在定点![]() 或
或![]() 以线段
以线段![]() 为直径的圆恒过该定点.
为直径的圆恒过该定点.
点睛:定点的探索与证明问题
(1)探索直线过定点时,可设出直线方程为![]() ,然后利用条件建立
,然后利用条件建立![]() 等量关系进行消元,借助于直线系的思想找出定点.
等量关系进行消元,借助于直线系的思想找出定点.
(2)从特殊情况入手,先探求定点,再证明与变量无关.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 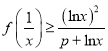 ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的任意三个顶点为顶点的三角形的面积是
的任意三个顶点为顶点的三角形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的右顶点,点
的右顶点,点![]() 在
在![]() 轴上.若椭圆
轴上.若椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用极坐标与直角坐标的互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
,消去参数![]() 可知曲线
可知曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,由直线
的圆,由直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得: ![]() ;则曲线C的方程为
;则曲线C的方程为![]() , 再次利用极坐标与直角坐标的互化公式可得
, 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面积的最大值.
面积的最大值.
试题解析:(1)由题意可知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:  ;可知曲线C的方程为
;可知曲线C的方程为![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
当![]() 时,
时, ![]() ,
,
所以△MON面积的最大值为![]() .
.
【题型】解答题
【结束】
23
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com