
分析 (1)设椭圆的方程,代入椭圆方程,即可求得m和n的值,求得椭圆的方程;
(2)设P点坐标,根据直线的斜率公式求得kBP•kBQ=-1,设直线PQ的方程,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得b=-$\frac{2}{3}$k,即可求得直线恒过定点.
解答 解:(1)设椭圆的方程为:mx2+ny2=1,(m>0,n>0),
则$\left\{\begin{array}{l}{m+\frac{3}{2}n=1}\\{2m+n=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{4}}\\{n=\frac{1}{2}}\end{array}\right.$,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)证明:设P点坐标(x,y),y2=$\frac{1}{2}$(4-x2),则A(-2,0),B(2,0),则
kAP=$\frac{y-0}{x+2}$,kBP=$\frac{y-0}{x-2}$,
则kAP•kBP=$\frac{{y}^{2}}{{x}^{2}-4}$=-$\frac{1}{2}$,
由kBQ=2kAP,故kBP•kBQ=-1.
∴直线BP与直线BQ的斜率乘积为-1为定值,
当直线PQ的斜率存在时,设lPQ:y=kx+b与x轴的交点为M,
$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=kx+b}\end{array}\right.$,整理得:(2k2+1)x2+4kbx+2b2-4=0,
设P(x1,y1),Q(x2,y2),则x1+x2=-$\frac{4kb}{2{k}^{2}+1}$,x1x2=$\frac{2{b}^{2}-4}{2{k}^{2}+1}$,
由kBP•kBQ=-1,即$\overrightarrow{BP}$•$\overrightarrow{BQ}$=0,则y1y2+x1x2-2(x1+x2)+4=0,
得(k2+1)x1x2+(kb-2)(x1+x2)+4+b2=0,
4k2+8kb+3b2=0,得b=-2k或b=-$\frac{2}{3}$k.y=k(x-2)或y=k(x-$\frac{2}{3}$),
所以过定点(2,0)或($\frac{2}{3}$,0),
A(2,0)为椭圆的右顶点,舍去,
∴直线PQ过定点($\frac{2}{3}$,0).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:选择题
将函数 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 的图象,若函数
的图象,若函数 在区间
在区间 和
和 上均单调递增,则实数
上均单调递增,则实数 的取值范围是 ( )
的取值范围是 ( )
A. 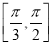 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:解答题
在△ 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)若 ,求角
,求角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在边长为1的正方体中ABCD-A1B1C1D1,P、Q分别是线段BD、C1C上的动点,则|PQ|的最小值是$\frac{\sqrt{2}}{2}$.
如图,在边长为1的正方体中ABCD-A1B1C1D1,P、Q分别是线段BD、C1C上的动点,则|PQ|的最小值是$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com