
分析 (Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=lnx+1,讨论f′(x)的符号,求出函数f(x)的单调区间,从而求得函数f(x)得极值;
(Ⅱ)当x$∈[\frac{1}{e},e]$时,由f(x)+$\frac{1}{2}$x2+ax+$\frac{3}{2}$≤0成立,得a$≤-lnx-\frac{x}{2}-\frac{3}{2x}$
记g(x)=-lnx-$\frac{x}{2}$-$\frac{3}{2x}$,x$∈[\frac{1}{e},e]$,
则g′(x)=-$\frac{1}{x}$-$\frac{1}{2}$+$\frac{3}{2{x}^{2}}$=-$\frac{(x+3)(x-1)}{2{x}^{2}}$,
利用导数求出g(x)在[$\frac{1}{e}$,e]上的最小值即可求得实数a的取值范围
解答 解:(Ⅰ)函数f(x)的定义域为(0,+∞),
∵f′(x)=lnx+1,令f′(x)=0得x=$\frac{1}{e}$,-----------------------------------------(2分)
当0$<x<\frac{1}{e}$时,f′(x)<0,当x$>\frac{1}{e}$时,f′(x)>0,
∴函数f(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增,----------------------------------------(4分)
∴函数f(x)无极大值,
当x=$\frac{1}{e}$时,函数f(x)在(0,+∞)有极小值,f(x)极小=f($\frac{1}{e}$)=-$\frac{1}{e}$,--------------------------(5分)
(Ⅱ)当x$∈[\frac{1}{e},e]$时,由f(x)+$\frac{1}{2}$x2+ax+$\frac{3}{2}$≤0成立,得a$≤-lnx-\frac{x}{2}-\frac{3}{2x}$,--------------(6分)
记g(x)=-lnx-$\frac{x}{2}$-$\frac{3}{2x}$,x$∈[\frac{1}{e},e]$,
则g′(x)=-$\frac{1}{x}$-$\frac{1}{2}$+$\frac{3}{2{x}^{2}}$=-$\frac{(x+3)(x-1)}{2{x}^{2}}$,
当x∈($\frac{1}{e}$,1)时,得g′(x)>0,当x∈(1,e)时,g′(x)<0
∴g(x)在($\frac{1}{e}$,1)上单调递增,在(1,e)上单调递减,---------------------------------------------------(9分)
又($\frac{1}{e}$)=1-$\frac{1}{2e}$-$\frac{3e}{2}$,g(e)=-1-$\frac{e}{2}$-$\frac{3}{2e}$,
∵g($\frac{1}{e}$)-g(e)=2+$\frac{1}{e}-e$<0,∴g($\frac{1}{e}$)<g(e),-------------------------------------------------(10分)
故g(x)在[$\frac{1}{e}$,e]上的最小值为g($\frac{1}{e}$),故只需a$≤g(\frac{1}{e}$),
即实数a的取值范围是(-∞,1-$\frac{1}{2e}$-$\frac{3e}{2}$].---------------------------------------------------(12分)
点评 本题考查了导数的应用,考查了利用导数处理含参函数恒成立问题,属于中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{{m}^{2}}$$+\frac{{y}^{2}}{{n}^{2}}$=1 | B. | $\frac{{x}^{2}}{{n}^{2}}$$+\frac{{y}^{2}}{{m}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{m}^{2}}$$+\frac{{y}^{2}}{{m}^{2}-{n}^{2}}$=1 | D. | $\frac{{x}^{2}}{{m}^{2}-{n}^{2}}$$+\frac{{y}^{2}}{{n}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若x=3,则x2=9”的否命题是:“若x=3,则x2≠9” | |
| B. | 若a=2且b=1,则a+b=3的逆否命题 | |
| C. | 命题:?x∈R,x2>0 | |
| D. | 命题:“?x∈R,使得sinx≥1”的否定是:“?x∈R,均有sinx≤1” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
选修4—1:几何证明选讲
如图,△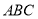 是圆
是圆 的内接三角形,
的内接三角形, 是
是 的延长线上一点,且
的延长线上一点,且 切圆
切圆 于点
于点 .
.

(1)求证: ;
;
(2)若 ,且
,且 ,求
,求 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com