
| A. | tan2$\frac{θ}{2}$<1 | B. | tan2$\frac{θ}{2}$>1 | C. | sin$\frac{θ}{2}$>cos$\frac{θ}{2}$ | D. | sin$\frac{θ}{2}$<cos$\frac{θ}{2}$ |
分析 利用诱导公式求得cosθ<0,sinθ>0,可得 θ∈(2kπ+$\frac{π}{2}$,2kπ+π),$\frac{θ}{2}$∈(kπ+$\frac{π}{4}$,kπ+$\frac{π}{2}$),从而得出结论.
解答 解:∵sin(θ+$\frac{π}{2}$)=cosθ<0,cos(θ-$\frac{π}{2}$)=sinθ>0,
∴θ∈(2kπ+$\frac{π}{2}$,2kπ+π),∴$\frac{θ}{2}$∈(kπ+$\frac{π}{4}$,kπ+$\frac{π}{2}$),
∴${tan}^{2}\frac{θ}{2}$>1,
故选:B.
点评 本题主要考查三角函数的化简求值,求得 $\frac{θ}{2}$∈(kπ+$\frac{π}{4}$,kπ+$\frac{π}{2}$),是解题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
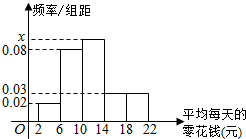 为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )
为了了解学生平均每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观,某校从高一年级1000名学生中随机抽取100名进行了调查,将所得数据整理后,画出频率分布直方图(如图),据此估计高一年级每天零花钱在[6,14)内的学生数为( )| A. | 780 | B. | 680 | C. | 648 | D. | 460 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B. | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | ||
| C. | |$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | 以上答案都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com