
���� ��������Բ�����ʵõ�a��b�Ĺ�ϵ��������Բ���̣���ֱ�߷����������������ĺ����꣬���ҳ��ý���������ʾ����a��ֵ����һ���õ�b��ֵ������Բ���̿���
�������A��D������ֱ�Ϊ��x1��y1����x1y1��0������x2��y2������A�������ʾB�����꣬��AB��AD��б�ʶ���A�������ʾ��д��ֱ��AD�ķ��̣�����Բ�������������ø���ϵ����ϵ�õ�AD��������ĺͣ����AD�е����꣬��BDб�ʿ�����д��BD����ֱ�߷��̣�ȡy=0�õ�M�����꣬��������б�ʵõ�AM��б�ʣ�����ֱ��б�ʵĹ�ϵ�õ��˵�ֵ��
��� �⣺����������֪��e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��a2-b2=c2��
��a2=4b2��
����ԲC�ķ��̿ɻ�Ϊx2+4y2=a2��
��y=x����ɵ�x=��$\frac{\sqrt{5}}{5}$a��
���$\sqrt{2}$•$\frac{2\sqrt{5}}{5}$a=$\frac{4\sqrt{10}}{5}$�����a=2����b=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1��
������A��x1��y1����x1y1��0����D��x2��y2����
��B��-x1��-y1����
��ֱ��AB��б��kAB=$\frac{{y}_{1}}{{x}_{1}}$��
��AB��AD��
��ֱ��AD��б��kAD=-$\frac{{x}_{1}}{{y}_{1}}$��
��AD����Ϊy=kx+m��
������֪k��0��m��0��
����$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$���ã�1+4k2��x2+8kmx+4m2-4=0��
��x1+x2=-$\frac{8km}{1+4{k}^{2}}$��
���y1+y2=k��x1+x2��+2m=$\frac{2m}{1+4{k}^{2}}$��
������ɵ�k1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{1}{4k}$=$\frac{{y}_{1}}{4{x}_{1}}$��
��ֱ��BD�ķ���Ϊy+y1=$\frac{{y}_{1}}{4{x}_{1}}$��x+x1����
��y=0����x=3x1����M��3x1��0����
�ɵ�k2=-$\frac{{y}_{1}}{2{x}_{1}}$��
��k1=-$\frac{1}{2}$k2������=-$\frac{1}{2}$��
��˴��ڳ�����=-$\frac{1}{2}$ʹ�ý��۳�����
���� ���⿼����Բ���̵�����Ҫ������ֱ������Բ��λ�ù�ϵ��Ӧ�ã�ֱ�����������������ݷ��̵ĸ���ϵ���Ĺ�ϵ���⣬�Ǵ��������������Ϊ���õķ�������Բ���ߵ��ص��Ǽ������Ƚϴ�Ҫ���Ծ߱���ǿ������������������


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
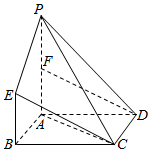 ��ͼ������ABCD�У�BC=2��AB=1��PA��ƽ��ABCD��BE��PA��BE=$\frac{1}{2}$PA��FΪPA���е㣮
��ͼ������ABCD�У�BC=2��AB=1��PA��ƽ��ABCD��BE��PA��BE=$\frac{1}{2}$PA��FΪPA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | -1��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| X | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 11 |
| A�� | 23�� | B�� | 24�� | C�� | 25�� | D�� | 26�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 27 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-y2=1 | B�� | $\frac{{x}^{2}}{2}$-y2=1 | C�� | x2-$\frac{{y}^{2}}{2}$=1 | D�� | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com