
【题目】已知定义在![]() 上的函数
上的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断![]() 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上是减函数(3)
上是减函数(3)![]()
【解析】试题分析:(1)由定义在实数集上的奇函数有![]() 列式求解,或直接由奇函数的定义得恒等式,由系数相等求解
列式求解,或直接由奇函数的定义得恒等式,由系数相等求解![]() 的值;(2)设
的值;(2)设![]() ,
, ![]() 且
且![]() ,可得
,可得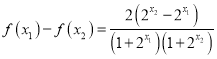 ,只需判断
,只需判断![]() ;(3)由函数的奇偶性和单调性,把给出的不等式转化为含有
;(3)由函数的奇偶性和单调性,把给出的不等式转化为含有![]() 的一元二次不等式,分离参数后求二次函数的最值,即可实数
的一元二次不等式,分离参数后求二次函数的最值,即可实数![]() 的取值范围.
的取值范围.
试题解析:(1)∵![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)![]() ,
, ![]() 在
在![]() 上是减函数.
上是减函数.
证明:设![]() ,
, ![]() 且
且![]() ,
,
则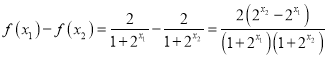 ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
即![]() ,∴
,∴![]() 在
在![]() 上是减函数.
上是减函数.
(3)不等式![]()
![]()
又![]() 是
是![]() 上的减函数,∴
上的减函数,∴![]() ,
,
∴![]() ,对
,对![]() 恒成立,
恒成立,
∴![]() .
.
【方法点晴】本题主要考查函数的奇偶性及单调性的应用,以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.
恒成立;④ 讨论参数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从装有n+1个球(其中n个白球,1个黑球)的口袋中取出m个球(0<m≤n,m,n∈N),共有 ![]() 种取法.在这
种取法.在这 ![]() 种取法中,可以分成两类:一类是取出的m个球全部为白球,共有
种取法中,可以分成两类:一类是取出的m个球全部为白球,共有 ![]() 种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有
种取法;另一类是取出的m个球有m﹣1个白球和1个黑球,共有 ![]() 种取法.显然
种取法.显然 ![]() ,即有等式:
,即有等式: ![]() 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子: ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 5 | 0 | -5 | 0 |
(1)求出实数![]() ;
;
(2)求出函数![]() 的解析式;
的解析式;
(3)将![]() 图像上所有点向左平移
图像上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 图像,求
图像,求![]() 的图像离原点
的图像离原点![]() 最近的对称中心.
最近的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又叫属相,是中国与十二地支相配以人出生年份的十二种动物,包括鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。已知在甲、乙、丙、丁、戊、己六人中,甲、乙、丙的属相均是龙,丁、戊的属相均是虎,己的属相是猴,现从这六人中随机选出三人,则所选出的三人的属相互不相同的概率等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产旅游纪念品的工厂,拟在2017年度进行系列促销活动,经市场调查和测算,该纪念品的年销售量 ![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用 ![]() (单位:万元)之间满足
(单位:万元)之间满足 ![]() 于
于 ![]() 成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知加工厂2017年生产纪念品的固定投资为3万元,没生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为“年平均每件生产成本的1.5倍”与“年平均每件所占促销费的一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知加工厂2017年生产纪念品的固定投资为3万元,没生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为“年平均每件生产成本的1.5倍”与“年平均每件所占促销费的一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(Ⅰ)请把该工厂2017年的年利润 ![]() (单位:万元)表示成促销费
(单位:万元)表示成促销费 ![]() (单位:万元)的函数;
(单位:万元)的函数;
(Ⅱ)试问:当2017年的促销费投入多少万元时,该工程的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只小船以![]() 的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以
的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以![]() 的速度前进(如图),现在小船在水平面上的
的速度前进(如图),现在小船在水平面上的![]() 点以南的40米处,汽车在桥上
点以南的40米处,汽车在桥上![]() 点以西的30米处(其中
点以西的30米处(其中![]() 水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).
水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)设Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com