
分析 (1)根据题意可知故函数f(x)的最小值为-$\frac{1}{e}$,利用导函数求出f(x)的最小值得出-$\frac{1}{ae}$=-$\frac{1}{e}$,a=1;
(2)不等式可转化为即lnx≤m(x-$\frac{1}{x}$),构造函数令h=lnx,n=m(x-$\frac{1}{x}$),分别求导,由题意可知,只需h'≥n',得出答案.
解答 解:(1)h(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,h'(x)=$\frac{1-x}{{e}^{x}}$,
∴函数在(-∞,1)上递增,在(1,+∞)上递减,
∴h(x)的最大值为h(1)=-$\frac{1}{e}$,
∵交集有且只有2个子集,
∴交集只有一个元素,故函数f(x)的最小值为-$\frac{1}{e}$,
∵f'(x)=ln(ax)+1,
∴a>0且x=$\frac{1}{ae}$时,f'(x)=0,
∴f(x)≥f($\frac{1}{ae}$)=-$\frac{1}{ae}$,
∴-$\frac{1}{ae}$=-$\frac{1}{e}$,
∴a=1;
(2)由题知f(x)=xlnx,
若f(x)≤m(x2-1)恒成立,即lnx≤m(x-$\frac{1}{x}$),
令h=lnx,n=m(x-$\frac{1}{x}$),
∴h'=$\frac{1}{x}$,n'=m(1+$\frac{1}{{x}^{2}}$),
∵x∈[1,+∞),
∴只需h'≥n',
∴m≥$\frac{x}{{x}^{2}+1}$,
∴m$≥\frac{1}{2}$.
点评 考查了集合的概念和导函数的利用,难点是函数的构造,求导.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
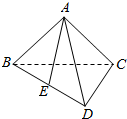 如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.
如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com