
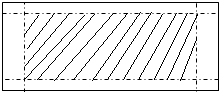
 为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小?
为了庆祝5月18日“世界博物馆日”,重庆白鹤梁水下博物馆对外宣传组需要张贴海报进行宣传,现让你设计一张如图所示的横向张贴的海报,要求版心(图中的阴影部分)面积为162dm2,上、下两边各空1dm,左、右两边各空2dm,如何设计版心的尺寸,才能使四周空白面积最小? 分析 利用版心面积设出一边长为xdm,表示出海报的总面积,四周空白面积最小即为海报的总面积最小,求面积最小可以利用基本不等式的思想.
解答 解:设“版心”的长为xdm,则版心的宽为$\frac{162}{x}$dm,此时四周空白面积为:
S=(x+4)($\frac{162}{x}$+2)-162=2x+$\frac{648}{x}$+8≥2$\sqrt{2x•\frac{648}{x}}$+8=80,
当且仅当2x=$\frac{648}{x}$,即x=18时四周空白面积最小.
答:当版心长为18dm,宽为9dm时,海报四周空白面积最小…(12分)
点评 本题考查建立函数模型解决实际问题的能力,考查基本不等式求函数最值的方法,考查学生的转化与化归能力,运算能力,方程思想,属于基本题型.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在[a,b]上不一定有最小值 | |
| B. | 函数f(x)在[a,b]上有最小值,但不一定是f(x0) | |
| C. | 函数f(x)在[a,b]上有最小值f(x0) | |
| D. | 函数f(x)在[a,b]上的最大值也可能是f(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 60°或120° | C. | 30° | D. | 30°或150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
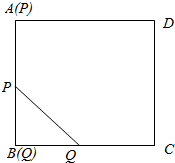 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com