Question

12．已知集合{（x，y）|x∈[0，3]，y∈[-1，1]}
（1）若x，y∈z，则3x+2y-1≥0概率为多少？
（2）若x，y∈R，则3x+2y-1≥0概率为多少？

Answer 1

分析 （1）由题意，x，y∈z，则x=0，1，2，3，y=-1，0，1，利用古典概型的概率公式解答；
（2）由x，y∈R，则是几何概型的概率求法，只要求出区域的面积以及满足条件的区域面积，利用面积比求概率．

解答 解：已知集合{（x，y）|x∈[0，3]，y∈[-1，1]}
（1）x，y∈z，则x=0，1，2，3，y=-1，0，1，从中任意取一个组成点（x，y），共有4×3=12个，而满足3x+2y-1≥0点共有10个，则由古典概型的公式得到$\frac{10}{12}=\frac{5}{6}$；
（2）x，y∈R，则满足题意的区域面积为6，而满足3x+2y-1≥0区域如图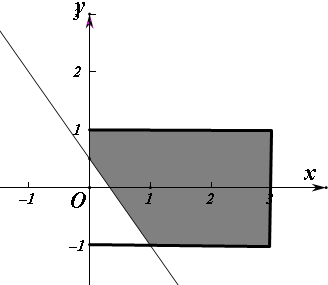面积为6-$\frac{1}{2}×\frac{3}{2}×1$，概率为1-$\frac{\frac{3}{4}}{6}$=$\frac{7}{8}$．

点评 本题主要考查几何概型中的面积类型和古典概型，两者最明显的区别是古典概型的基本事件是有限的，几何概型的基本事件是无限的．