
分析 (1)利用待定系数法求道路车流密度M与大气能见度x的函数解析式;
(2)根据题意,函数F(x)表达式为分段函数的形式;
(3)由(2),分段求最值,即可得出结论.
解答 解:(1)设道路车流密度M与大气能见度x的函数解析式为M(x)=kx+b,
由题意,$\left\{\begin{array}{l}{100k+b=160}\\{500k+b=80}\end{array}\right.$,∴k=-$\frac{1}{5}$,b=180,
∴M(x)=-$\frac{1}{5}$x+180,x≥100;
(2)∵车流量=行车速度×车流密度,
∴F(x)=$\left\{\begin{array}{l}{(\frac{1}{10}x+10)(-\frac{1}{5}x+180)=-\frac{1}{50}{x}^{2}+16x+1800,100≤x<800}\\{90(-\frac{1}{5}x+180)=-18x+16200,x≥800}\end{array}\right.$;
(3)当100≤x<800时,F(x)=-$\frac{1}{50}$(x-400)2+5000,
当x=400时,其最大值为5000,
当x≥800时,F(x)=-18x+16200为减函数,
∴当x=800时,其最大值为1800.
综上,当大气能见度为400米时,车流密度会达到最大值,最大值为5000辆/小时.
点评 本题给出车流密度的实际问题,求车流密度最大值及相应的车流密度,着重考查了函数、最值等基础知识,同时考查运用数学知识解决实际问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
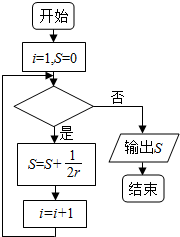
| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com