
分析 (1)作差(作商),即可比较证明大小;
(2)作差比较即可证明;由不等式(a2+b2)(x2+y2)≥(ax+by)2成立知$({sin^2}x+{cos^2}x)(\frac{1}{{{{sin}^2}x}}+\frac{4}{{{{cos}^2}x}})≥9$,即可得出结论.
解答 解:(1)log23-log34=$\frac{lg3}{lg2}-\frac{lg4}{lg3}$=$\frac{l{g}^{2}3-lg2lg4}{lg2lg3}$>$\frac{l{g}^{2}3-(\frac{lg2+lg4}{2})^{2}}{lg2lg3}$>$\frac{l{g}^{2}3-(\frac{1}{2}lg9)^{2}}{lg2lg3}$=0,
所以log23>log34
同理log34>log45,
一般性的结论:logn(n+1)>log(n+1)(n+2).(n∈N+)
$\frac{lo{g}_{(n+1)}(n+2)}{lo{g}_{n}(n+1)}$=log(n+1)(n+2)log(n+1)n<$[\frac{lo{g}_{(n+1)}(n+2)n}{2}]^{2}$<1,
∵logn(n+1)>0,∴logn(n+1)>log(n+1)(n+2).(n∈N+);
(2)∵(a2+b2)(x2+y2)-(ax+by)2=a2x2+a2y2+b2x2+b2y2-(a2x2+2abxy+b2y2)=a2y2-2abxy+b2x2=(ay-bx)2≥0∴(a2+b2)(x2+y2)≥(ax+by)2
由不等式(a2+b2)(x2+y2)≥(ax+by)2成立
知$({sin^2}x+{cos^2}x)(\frac{1}{{{{sin}^2}x}}+\frac{4}{{{{cos}^2}x}})≥9$,
∴(sin2x+cos2x)($\frac{1}{{{{sin}^2}x}}$+$\frac{4}{{{{cos}^2}x}}$)的最小值为9.
点评 本题考查合情推理,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a-b}$+$\frac{1}{b-c}$>$\frac{4}{a-c}$ | B. | $\frac{1}{a-b}$+$\frac{1}{b-c}$<$\frac{4}{a-c}$ | C. | $\frac{1}{a-b}$+$\frac{1}{b-c}$≥$\frac{4}{a-c}$ | D. | $\frac{1}{a-b}$+$\frac{1}{b-c}$≤$\frac{4}{a-c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
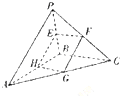 三棱锥P-ABC中,PA=2,BC=3,PA⊥BC,如图所示,作与PA、BC都平行的截面,分别交棱PB、BC、AC、AB于点E、F、G、H,则截面EFGH的最大面积为( )
三棱锥P-ABC中,PA=2,BC=3,PA⊥BC,如图所示,作与PA、BC都平行的截面,分别交棱PB、BC、AC、AB于点E、F、G、H,则截面EFGH的最大面积为( )| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com